Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B.
A = 4xn-2 -5x3
B = 2x3
Những câu hỏi liên quan
. Đơn thức -8x3 y2z3t3 chia hết cho đơn thức nào?A. -2x3 y3z3t4. B. -9x3 yz2t 2.C. 4x4 y2zt2. D. 2x3 y2z2t4.Câu 132. Giá trị của số tự nhiên n để phép chia xn+3 y6 : x9 yn là phép chia hết? A. n 6. B. n 5. C. n 6. D. n 6.
Đọc tiếp
. Đơn thức -8x3 y2z3t3 chia hết cho đơn thức nào?
A. -2x3 y3z3t4.
B. -9x3 yz2t 2.
C. 4x4 y2zt2.
D. 2x3 y2z2t4.
Câu 132. Giá trị của số tự nhiên n để phép chia xn+3 y6 : x9 yn là phép chia hết?
A. n < 6.
B. n = 5.
C. n > 6.
D. n = 6.
Bài 5. (0,5 điểm) Cho đa thức A 4x9y2n+10x10y5z24�9�2�+10�10�5�2 và đơn thức B 2x3ny42�3��4. Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B.
Đọc tiếp
Bài 5. (0,5 điểm) Cho đa thức A = và đơn thức B = . Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B.
Để A ⋮ B thì:
3n ≤ 9 và 2n ≥ 4
n ≤ 3 và n ≥ 2
n = 2 hoặc n = 3
Đúng 0
Bình luận (0)
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7 x n - 1 y 5 - 5 x 3 y 4 ; B = 5 x 2 y n
Ta có
A : B = ( 7 x n - 1 y 5 - 5 x 3 y 4 ) : ( 5 x 2 y n ) = 7 / 5 x n - 3 y 5 - 5 - x y 4 - n
Theo đề bài đa thức A chia hết cho đơn thức B
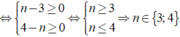
Vậy giá trị n cần tìm là n∈{3; 4}
Đúng 0
Bình luận (0)
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7 x n - 1 y 5 - 5 x 3 y 4 ;
B = 5 x 2 y n
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B:a) A
14
x
8
y
4
-
9
x
2
n
y
6
; B
-
2
x
7
y
n
; b) A
4
x
9...
Đọc tiếp
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B:
a) A = 14 x 8 y 4 - 9 x 2 n y 6 ; B = - 2 x 7 y n ;
b) A = 4 x 9 y 2 n + 9 x 8 y 5 z ; B = 3 x 3 n y 4 .
Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B:
A=7n^n-1.y^5 - 5x^3y^4
B=5x^2y^2
Tìm số tự nhiên n để đa thức M chia hết cho đơn thức N:a) M
-
8
y
12
z
10
-
21
y
20
z
2
n
-
1
; N
-
6
y
2
n
z
9...
Đọc tiếp
Tìm số tự nhiên n để đa thức M chia hết cho đơn thức N:
a) M = - 8 y 12 z 10 - 21 y 20 z 2 n - 1 ; N = - 6 y 2 n z 9 ;
b) M = 2 3 x 3 n + 1 y 5 z 6 + 3 x 14 y 6 z 4 ; N = 1 7 x 13 y 5 z 2 n - 5 .
Tìm số a để đa thức 2x3 – 3x2 + x + a chia hết cho đa thức x + 2.
Thực hiện phép chia:
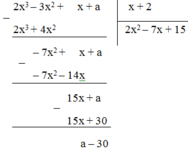
2x3 – 3x2 + x + a chia hết cho x + 2
⇔ số dư = a – 30 = 0
⇔ a = 30.
Cách 2: Phân tích 2x3 – 3x2 + x + a thành nhân tử có chứa x + 2.
2x3 – 3x2 + x + a
= 2x3 + 4x2 – 7x2 – 14x + 15x + 30 + a – 30
(Tách -3x2 = 4x2 – 7x2; x = -14x + 15x)
= 2x2(x + 2) – 7x(x + 2) + 15(x + 2) + a – 30
= (2x2 – 7x + 15)(x + 2) + a – 30
2x3 – 3x2 + x + a chia hết cho x + 2 ⇔ a – 30 = 0 ⇔ a = 30.
Đúng 1
Bình luận (0)
Tìm số a để đa thức 2x3-3x2+x+a chia hết cho đa thức x+2
Số dư của phép chia đa thức \(\text{f( x ) = 2x^3 - 3x^2 + x + a}\) cho \(\text{x + 2}\) là
\(\text{f ( -2 ) = 2(-2) ^3 - 3 (-2 )^2 + ( - 2 ) + a = -30 + a}\)
Để phép chia là chia hết thì số dư bằng \(\text{0}\)
Hay \(\text{-30 + a = 0}\) \(\Rightarrow\) \(\text{a = 30}\)
Đúng 4
Bình luận (0)
