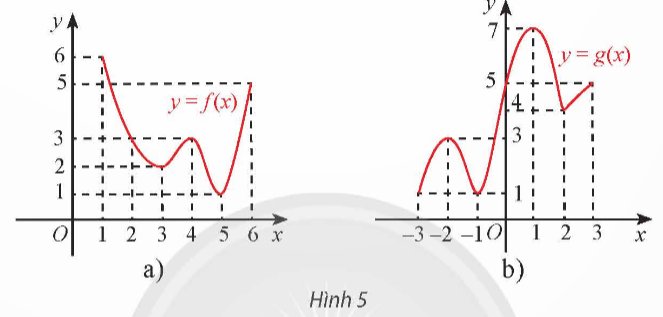
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 5.
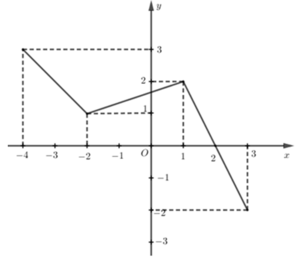
Cho đồ thị hàm số có đồ thị (C) (hình vẽ). Tìm tổng giá trị lớn nhất và nhỏ nhất của hàm số trên [−4;2]
A. 5
B. 3
C. 0
D. 1
Cho hàm số y = f ( x ) xác định và liên tục trên ℝ , có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f ( x ) trên đoạn - 2 ; 2
 .
.
A. m = -5, M = 0
B. m = -5, M = -1
C. m = -1, M = 0
D. m = -2, M = 2
Nhận thấy trên đoạn [-2;2]
● Đồ thị hàm số có điểm thấp nhất có tọa độ (-2;-5) và (1;-5)
=> giá trị nhỏ nhất của hàm số này trên đoạn [-2;2] bằng - 5
● Đồ thị hàm số có điểm cao nhất có tọa độ (-1;1) và (-2;1)
=> giá trị lớn nhất của hàm số này trên đoạn [-2;2] bằng -1.
Chọn B.
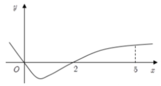
Cho hàm số f x có đạo hàm là f ' x . Đồ thị của hàm số y = f ' x được cho như hình vẽ bên. Biết rằng f 0 + f 3 = f 2 + f 5 . Giá trị nhỏ nhất và giá trị lớn nhất của f x trên đoạn [ 0 ; 5 ] lần lượt là
A. f 0 , f 5
B. f 2 , f 0
C. f 1 , f 5
D. f 2 , f 5
Đáp án D
Từ đồ thị y = f ' x trên đoạn [ 0 ; 5 ] , ta có bảng biến thiên của hàm số y = f x như hình vẽ bên
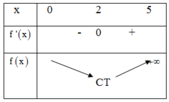
Suy ra min 0 ; 5 f x = f 2 .
Từ giả thiết, ta có
f 0 + f 3 = f 2 + f 5 ⇔ f 5 − f 3 = f 0 − f 2
Hàm số f(x) đồng biến trên 2 ; 5
⇒ f 3 > f 5 ⇒ f 5 − f 2 > f 5 − f 3 = f 0 − f 2 ⇔ f 5 > f 0
Suy ra max 0 ; 5 f x = f 0 ; f 5 = f 5
Cho hàm số y = f x liên tục trên ℝ và có đồ thị như hình bên. Tổng giá trị lớn nhất, giá trị nhỏ nhất của hàm số g x = f 2 sin x 2 cos x 2 + 3 bằng

A. 6
B. 8
C. 4
D. 5
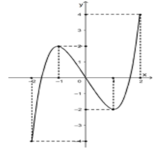
Cho hàm số y = f(x) có đồ thị như hình vẽ. Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2;1] lần lượt là M, m. Giá trị M + m bằng
A. 2
B. -2
C. 0
D. 4
Chọn B
Từ đồ thị suy ra M = 2 và m = -4.
Vậy M + m = 2 - 4 = -2.
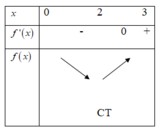
Cho hàm số f(x) có đạo hàm là f ' x . Đồ thị của hàm số y = f ' x được cho như hình vẽ bên. Biết rằng f 0 + f 3 = f 2 + f 5 . Giá trị nhỏ nhất và giá trị lớn nhất của f(x) trên đoạn 0 ; 5 lần lượt là

A. f 0 , f 5
B. f(2); f(0)
C. f(1); f(5)
D. f(2); f(5)
Đáp án D
Từ đồ thị y = f ' x trên đoạn 0 ; 5 , ta có bảng biến thiên của hàm số y = f x như hình vẽ bên
Suy ra min 0 ; 5 f x = f 2 . Từ giả thiết, ta có
f 0 + f 3 = f 2 + f 5 ⇔ f 5 − f 3 = f 0 − f 2
Hàm số f(x) đồng biến trên 2 ; 5
⇒ f 3 > f 2 ⇒ f 5 − f 2 > f 5 − f 3
= f 0 − f 2 ⇔ f 5 > f 0
Suy ra
max 0 ; 5 f x = f 0 , f 5 = f 5
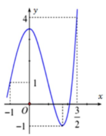
Cho hàm số y = f x liên tục trên ℝ và có đồ thị như hình vẽ. Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x trên - 1 ; 3 2 . Giá trị của M - N bằng
![]()
![]()
![]()
Cho hàm số y = f x liên tục trên R và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x trên - 1 ; 3 2 . Giá trị của M – m bằng
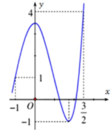
A. 1 2
B. 5
C. 4
D. 3
Chọn đáp án B.
Quan sát đồ thị có M = 4; m = -1
⇒ M - m = 5
Cho hàm số y = f(x) có đồ thị như hình vẽ. Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-1;6]. Tính giá trị biểu thức
P = 2M+3N
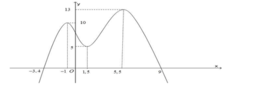
A. 8
B. 41
C. 49
D. 18
Cho hàm số y=f(x), x ∈ - 2 ; 3 có đồ thị như hình vẽ. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) trên đoạn - 2 ; 3 . Giá trị của M+n là
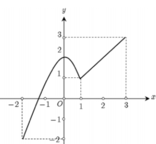
A. 6
B. 1
C. 5
D. 3