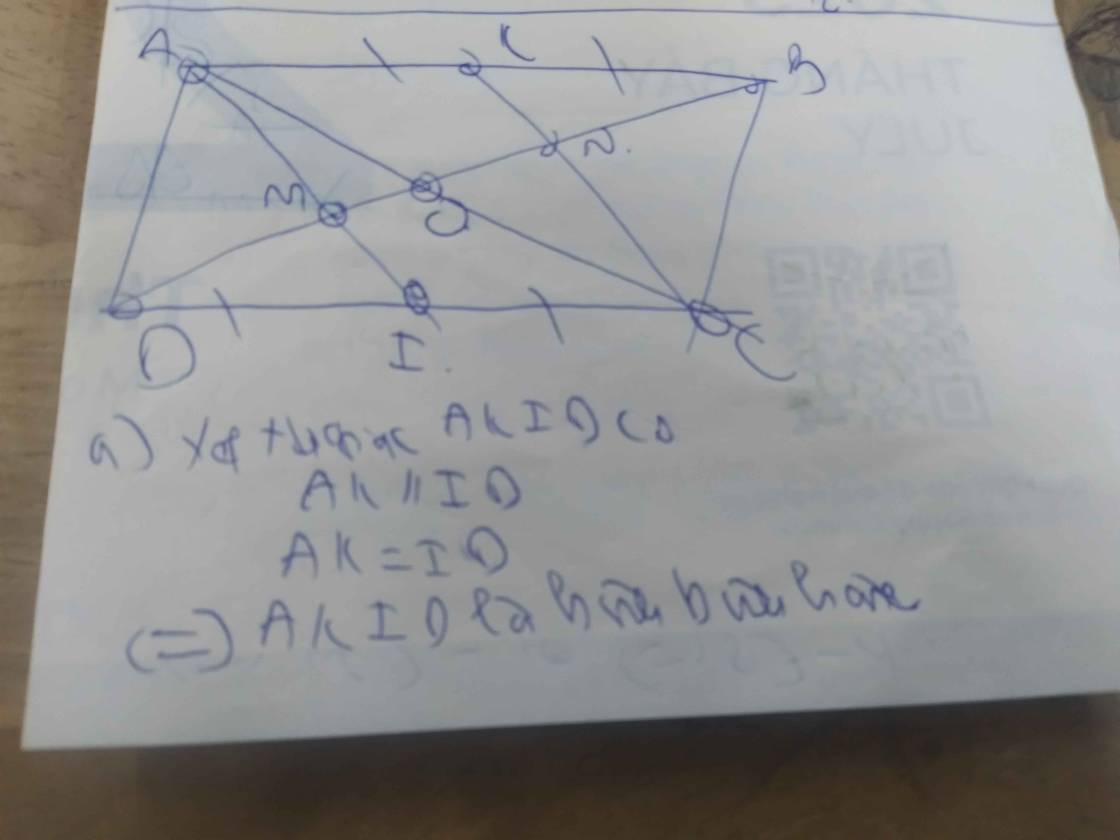
Cho Hình bình hành ABCD có K,I là trung điểm của AB,CD.M,N là giao điểm của AI,CK,BD C/m a) AI // CK b) C/m AKID là hình bình hành c) C/m DM=BN

Những câu hỏi liên quan
cho hình bình hành ABCD có K là trung điểm AB,I là trung điểm CD.BD lần lượt cắt AI và CK tại M và N. Gọi O là giao điểm của hai đường chéo AC và BD.
a)Tứ giác AKID,BKIC,AKCI là hình gì
b)c/m DM=MN=NB
c)I,O,K thằng hàng
d)AI cắt DK tại E,BI cắt CK tại F, c/m KEIF là hình bình hành và FE =AK
Cho hình bình hành ABCD. Gọi I, K lần lượt là trung điểm của các cạnh AB và CD, M và N là giao diểm của AI và CK với BD.
a) CM: AI // CK
b) CM: DM = MN = NB
Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của AB và CD, M và N là giao điểm của AI và CK với BD
a) Chứng minh : AI song song với CK
b) Chứng minh DM=MN=NB
a ) AK = 1/2 AB
CI = 1/2 CD
Mà AB //= CD nên AK //= CI suy ra
AKCI - hình bình hành
Nên AI // CK
b ) Xét t/g DNC có :
I là trung điểm CD mà IM // NC
=> IM là đường trung bình của t/g DNC
=> MD = MN ( 1 )
Xét t/g ABM có :
K là trung điểm AB mà KN // AM
=> KN là đường trung bình của t/g ABM ( 2 )
Từ ( 1 ) ; ( 2 ) suy ra DM = MN = NB
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB
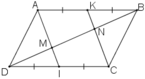
a) + K là trung điểm của AB ⇒ AK = AB/2.
+ I là trung điểm của CD ⇒ CI = CD/2.
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = CD/2 hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI//KC hay MI//NC.
ΔDNC có: DI = IC, IM // NC ⇒ DM = MN (1)
+ AI // KC hay KN//AM
ΔBAM có: AK = KB, KN//AM ⇒ MN = NB (2)
Từ (1) và (2) suy ra DM = MN = NB.
Đúng 3
Bình luận (0)
cho hình bình hành ABCD. Gọi I,K theo thứ tự là trung điểm của CD,AB. Đường chéo BD cắt AI,CK theo thứ tự ở M và N. O là trung điểm của MN. Chứng minh:
a) AI//CK
b) DM=MN=NB
c) 3 điểm K,O,I thẳng hàng
Giúp mình câu c với ạ. Mình cần gấp.
hình bình hành ABCD.Gọi K và I lần lượt là trung điểm của AB và CD.M và N lần lượt là giao điểm của AI và CK với BD.CMR:
a,tam giác AND bằng tam giác CNB
b, góc MAC bằng góc NCA và AI//KC
c,DM=MN=NB
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo
BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK b) DM = MN = NB
Giải :
a) + K là trung điểm của AB ⇒ AK = \(\frac{AB}{2}\).
+ I là trung điểm của CD ⇒ CI = \(\frac{CD}{2}\).
+ ABCD là hình bình hành
⇒ AB // CD hay AK // CI
và AB = CD ⇒ AB/2 = \(\frac{CD}{2}\) hay AK = CI
+ Tứ giác AKCI có AK // CI và AK = CI
⇒ AKCI là hình bình hành.
b) + AKCI là hình bình hành
⇒ AI // KC hay \(\frac{MI}{NC}\).
\(a)\)
\(K\)là trung điểm \(AB\)\(\Rightarrow AK=\frac{AB}{2}\)
\(I\)là trung điểm \(CD\)\(\Rightarrow CI=\frac{CD}{2}\)
Mà theo đề ra: \(ABCD\)là hình bình hành
\(\Rightarrow AB//CD\)hay \(AK//CI\)
\(\Rightarrow AB=CD\Rightarrow\frac{AB}{2}=\frac{CD}{2}\)hay \(AK=CI\)
Tứ giác \(AKCI\)có \(AK//CI\)\(;\)\(AK=CI\)
\(\Rightarrow AKCI\)là hình bình hành
\(b)\)
Theo phần a), ta có: \(AKCI\)là hình bình hành
\(\Rightarrow AI//KC\)hay \(MI//NC\)
Bài 3. Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của các cạnh AB và CD, M và N là giao điểm của đường thẳng AI và đường thẳng CK với đường thẳng BD.
a) Chứng minh: AI // CK .
b) Chứng minh: DM = MN = NB
a: AB//CD
mà I∈AB
và K∈CD
nên AI//CK
Đúng 1
Bình luận (0)
a) Ta có: AK = 1212 AB
IC = 1212 DC
mà AB = DC (vì ABCD là hình bình hành)
=> AK = IC
=> AK // IC (vì AB // DC)
=> AKCI là hình bình hành
=> AI // KC
b) Xét ΔABMΔABM có:
AK = KB (gt)
AM // KN (vì AI // KC)
=> BN = MN (1)
Xét ΔDNCΔDNC có:
DI = IC (gt)
IM // CN (vì AI // KC)
=> DM = MN (2)
Từ 1 và 2 =>DM=MN=NB
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. K,I lần lượt là trung điểm AB và CD. M,N lần lượt là giao điểm AI và CK với BD
Chứng minh:
a) Tam giác ADM = tam giác CBN
b) Góc MAC= góc NCA và IN//CN
c) DM=MN=NB
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng :
a)Tứ giác AICK là hình bình hành.
b) AI // CK.
c) DM = MN = NB.
a: Xét tứ giác AICK có
AK//CI
AK=CI
Do đó: AICK là hình bình hành
Đúng 0
Bình luận (0)