Cho hình lăng trụ ABC.A'B'C' (H.5.25). Trong các vectơ có điểm đầu và điểm cuối đều là đỉnh của hình lăng trụ, những vectơ nào là vectơ chỉ phương của đường thẳng AB?
Những câu hỏi liên quan
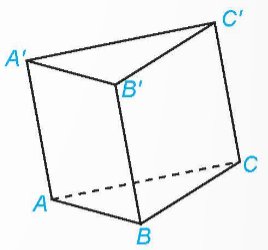
Nhắc lại định nghĩa vectơ không gian.
Cho hình lăng trụ tam giác ABC.A'B'C'. Hãy kể tên những vectơ bằng vectơ A A ' → có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.
Vectơ trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
Đúng 0
Bình luận (0)
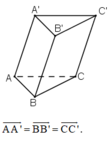
Nhắc lại định nghĩa vectơ trong không gian.
Cho hình lăng trụ tam giác ABC.A'B'C'. Hãy kể tên những vectơ bằng vectơ \(\overrightarrow{AA'}\) có điểm đầu và điểm cuối là đỉnh của lăng trụ ?
Vectơ trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
Vì các cạnh bên của hình lăng trụ là các đoạn thẳng song song và bằng nhau nên các vectơ bằng vectơ và có điểm đầu và điểm cuối là đỉnh của hình lăng trụ là: các vector BB', CC', DD'.
Đúng 0
Bình luận (0)
Cho hình lăng trụ tứ giác ABCD.ABCD. Mặt phẳng (P) cắt các cạnh bên AA, BB, CC, DDlần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ. Hãy chỉ ra các vectơ:
Đọc tiếp
Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Mặt phẳng (P) cắt các cạnh bên AA', BB', CC', DD'lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của hình lăng trụ. Hãy chỉ ra các vectơ:
Cho hình lăng trị tứ giác ABC.ABCD. Mặt phẳng (P) cắt các cạnh bên AA, BB,CC, DD lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của lăng trụ. Hãy chỉ ra các vectơ :
a) Cùng phương với overrightarrow{IA}
b) Cùng hướng với overrightarrow{IA}
c) Ngược hướng với overrightarrow{IA}
Đọc tiếp
Cho hình lăng trị tứ giác ABC.A'B'C'D'. Mặt phẳng (P) cắt các cạnh bên AA', BB',CC', DD' lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của lăng trụ. Hãy chỉ ra các vectơ :
a) Cùng phương với \(\overrightarrow{IA}\)
b) Cùng hướng với \(\overrightarrow{IA}\)
c) Ngược hướng với \(\overrightarrow{IA}\)
a) Các véctơ cùng phương với là:
,
,
,
,
,
,
.
b) Các véctơ cùng hướng với là:
,
,
.
c) Các véctơ ngược hướng với là:
,
,
,
.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho hình lăng trụ tam giác đều
A
B
C
.
A
1
B
1
C
1
có
A
1
3
;
-
1
;
1
. hai đỉnh B, C thuộc trục Oz và
A
A...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hình lăng trụ tam giác đều A B C . A 1 B 1 C 1 có A 1 3 ; - 1 ; 1 . hai đỉnh B, C thuộc trục Oz và A A 1 = 1 (C không trùng O). Biết u → = a ; b ; 2 là một vectơ chỉ phương của đường thẳng A 1 C . Tính T = a 2 + b 2
A. T = 4
B. T = 5
C. T = 9
D. T = 16
Gọi I là trung điểm của BC. Ta chứng minh được 
Suy ra I là hình chiếu của A 1 trên BC nên I(0;0;1)
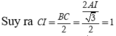
Chọn VTCP của 
Chọn D.
Đúng 0
Bình luận (0)
Cho hình lục giác ABCDEF có o là tâm.hãy xác định các vectơ mà có điểm đầu và điểm cuối là đỉnh của lục giác đều và tâm o sao cho bằng vectơ AB
Chắc là lục giác đều?
Các vecto bằng \(\overrightarrow{AB}\) là \(\overrightarrow{FO};\overrightarrow{OC};\overrightarrow{ED}\)
Đúng 1
Bình luận (1)
Cho hình lăng trụ
A
B
C
.
A
B
C
có đáy ABC là tam giác đều cạnh 2a. biết thể tích của khối lăng trụ
A
B
C
.
A
B
C
bằng
a
3
. Khoảng cách h giữa hai đường thẳng AB và BC bằng A.
4
a...
Đọc tiếp
Cho hình lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh 2a. biết thể tích của khối lăng trụ A B C . A ' B ' C ' bằng a 3 . Khoảng cách h giữa hai đường thẳng AB và B'C' bằng
A. 4 a 3
B. a 3
C. a
D. a 3
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh 2a, biết thể tích của khối lăng trụ ABC.ABC bằng
a
3
. Tính khoảng cách h giữa hai đường thẳng AB và BC.
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh 2a, biết thể tích của khối lăng trụ ABC.A'B'C' bằng a 3 . Tính khoảng cách h giữa hai đường thẳng AB và B'C'.
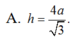
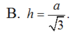
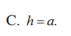
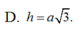
Cho lục giác đều ABCDEF tâm O. Hãy chỉ ra các vectơ bằng vectơ AB có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác.
Cho lăng trụ tam giác đều ABC.ABC có cạnh đáy bằng a và có đường cao h
a) Một hình trục có các đường tròn đáy tiếp xúc với các cạnh của tam giác đáy được gọi là hình trụ nội tiếp trong lăng trụ. Hãy tính diện tích xung quanh của hình trụ nội tiếp đó ?
b) Gọi I là trung điểm của cạnh BC. Đường thẳng AI cắt hình trụ nội tiếp nói trên theo một đoạn thẳng. Tính độ dài đoạn thẳng đó ?
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a và có đường cao h
a) Một hình trục có các đường tròn đáy tiếp xúc với các cạnh của tam giác đáy được gọi là hình trụ nội tiếp trong lăng trụ. Hãy tính diện tích xung quanh của hình trụ nội tiếp đó ?
b) Gọi I là trung điểm của cạnh BC. Đường thẳng A'I cắt hình trụ nội tiếp nói trên theo một đoạn thẳng. Tính độ dài đoạn thẳng đó ?
Ta có : \(\dfrac{KM}{AA'}=\dfrac{IK}{IA}=\dfrac{2}{3}\Rightarrow KM=\dfrac{2}{3}h\)
Xét tam giác vuông IKM ta có : \(IM^2=IK^2+KM^2=\dfrac{3a^2}{9}+\dfrac{4h^2}{9}=\dfrac{3a^2+4h^2}{9}\)
Vậy :
\(IM=\dfrac{\sqrt{3a^2+4h^2}}{3}\)
Đúng 0
Bình luận (0)