Tìm giao của hai tập hợp N và N*

Những câu hỏi liên quan
Tìm giao của hai tập hợp N và N*
Ta có: N ={0; 1; 2; 3; 4; ...}.
Và N* = {1; 2; 3; 4; ...}
Ta thấy mọi phần tử của tập hợp N* đều thuộc tập N.
Do đó, N ∩ N* = N*
Đúng 0
Bình luận (0)
tìm giao của hai tập hợp N và N*
Xem thêm câu trả lời
Gọi tập hợp H là giao của hai tập hợp B(5) và Ư(20).Tìm số tự nhiên n biết n∈H và n là số lẻ
B(5) = { 0 ; 5 ; 10 ; 15 ; 20 ; .... }
Ư(20) = { 1 ; 2 ; 4 ; 5 ; 10 ; 20 }
Vì n \(\in\)H và B là số lẻ nên n = 5
Đúng 0
Bình luận (0)
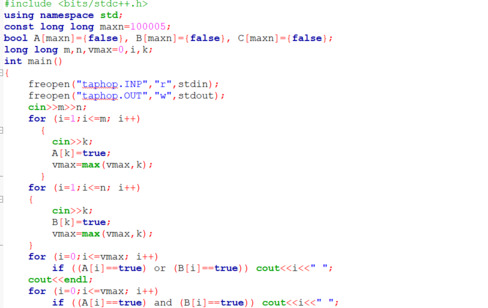
Cho tập hợp A gồm n phần tử là a1, a2, ..., an, và tập hợp B gồm m phần tử là b1, b2, ...,
bm.
Nhiệm vụ của bạn là hãy tìm số lượng của 2 tập hợp:
- Tập hợp thứ nhất là hợp của hai tập hợp A và B
- Tập hợp thứ hai là giao của hai tập hợp A và B
(lập trình pascal)
Tìm giao của hai tập hợp N và N*
làm nhanh và đầy đủ mik tick luôn nha
Mọi số trừ số không đều là giao
Vì những số đó có cả ở hai tập hợp
Đ/s:..................
**** nha
Đúng 0
Bình luận (0)
N = { 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; ... }
N* = { 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; ... }
N = số từ 0 đến tiếp theo như thế
N* = Ko có số 0
Đúng 0
Bình luận (0)
Mọ số tự nhiên(trừ số 0) là giao điểm của hai tập hợp N và N*
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tập hợp Z và tập hợp N. Tìm giao của Z và N
Giao của tập hợp Z và N chính là tập hợp N, vì N là tập hợp con của tập hợp Z
Đúng 0
Bình luận (0)
Tìm giao của hai tập hợp \(\mathbb{N}\) và \(\mathbb{N}^{\circledast}\) ?
\(N=\left\{0;1;2;3;...\right\}\\ N^{\circledast}=\left\{1;2;3;4;...\right\}\\ N\cap N^{\circledast}=\left\{1;2;3;4;...\right\}\\\Leftrightarrow N\cap N^{\circledast}=N^{\circledast}\)
Đúng 0
Bình luận (0)
giao của tập hợp N và tập hợp N* là tập hợp N*
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm giao của 2 tập hợp N và N*
Giao của 2 tập hợp N và N* bằng {1 ; 2 ; 3 ; 4 ; ...}
Đúng 0
Bình luận (0)
Tìm giao của hai tập hợp: A = { n thuộc N: n là ước của 18} B = { m thuộc N: m là ước của 36 }
A = { 1; 2; 3; 6; 9; 18 }
B = { 1; 2; 3; 4; 6; 9; 12; 18; 36 }
=> A n B = { 1; 2; 3; 6; 9; 18 }
2 tập hợp giao nhau mình tạm kí hiệu là n nhé!
Đúng 0
Bình luận (0)