Giải phương trình nghiệm nguyên:
x3 – y3 – 2y2 – 3y – 1 = 0
Cho phương trình 2 y 2 − 3 y + 7 − m = − 2 y 2 + 6 − y 3 . Tìm giá trị của tham số m để phương trình nhận y=-3 là nghiệm.
Trong các giá trị y = 0 và y = 1, đâu là nghiệm của phương trình 2 y 2 − 3 y + 5 = 5 2 y − 1 − 2 3 y + 1 ?
y = 0 không là nghiệm và y = 1 là nghiệm của PT đã cho.
Trong các giá trị y = 0 và y = -2, đâu là nghiệm của bất phương trình 3 ( y − 1 ) + y − 3 ≥ 1 + 2 y 2 + 3 y ?
Ta có y = 0 không phải là nghiệm, còn y = -2 là nghiệm của BPT.
1) Tìm nghiệm nguyên của phương trình : x2= 2y2+2013
2) Giải phương trình x3+2x2- 4x +\(\dfrac{8}{3}\)=0
Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).
Giải phương trình nghiệm nguyên:
3x2 + 5xy - 8x -2y2 - 9y - 4 = 0
Lời giải:
PT $\Leftrightarrow 3x^2+x(5y-8)-(2y^2+9y+4)=0$
Coi đây là pt bậc 2 ẩn $x$. Để pt có nghiệm nguyên thì:
$\Delta=(5y-8)^2+12(2y^2+9y+4)=t^2$ với $t\in\mathbb{N}$)
$\Leftrightarrow 49y^2+28y+112=t^2$
$\Leftrightarrow (7y+2)^2+108=t^2$
$\Leftrightarrow 108=(t-7y-2)(t+7y+2)$
Đến đây là dạng phương trình tích đơn giản rồi. Bạn chỉ cần xét TH. Lưu ý rằng $t+7y+2>0$ và $t-7y-2, t+7y+2$ có cùng tính chẵn lẻ.
Giải phương trình nghiệm nguyên 6x²+2y2-7xy +14x-9y-21=0
Cho hệ phương trình 2 x + 3 y = 7 2 − m 4 x − y = 5 m . Có bao nhiêu giá trị của m mà m > 1 2 để hệ phương trình có nghiệm thỏa mãn: x 2 + 2 y 2 = 25 16
A. 0
B. 1
C. 2
D. 3
Ta có
2 x + 3 y = 7 2 − m 4 x − y = 5 m ⇔ 4 x + 6 y = 7 − 2 m 4 x − y = 5 m ⇔ 7 y = 7 − 7 m 4 x − y = 5 m ⇔ y = 1 − m 4 x − 1 − m = 5 m ⇔ y = 1 − m x = 4 m + 1 4
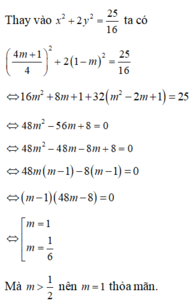
Đáp án: B
Số nghiệm của hệ phương trình x 3 = x + 3 y y 3 = y + 3 x là:
A. 2
B. 3
C. 1
D. 4
Số nghiệm của hệ phương trình x 3 - 3 y = y 3 - 3 x x 6 + y 6 = 27 là:
A. 1
B. 2
C. 6
D. 3
Đáp án: B



Vậy hệ phương trình có 2 nghiệm.
giải phương trình nghiệm nguyên 3x^2+3xy+3y^2=x+8y
giải phương trình nghiệm nguyên 2x^2+3y^2-5xy+3x-2y-3=0
Với câu a)bạn nhân cả 2 vế cho 12 rồi ép vào dạng bình phương 3 số
Câu b)bạn nhân cho 8 mỗi vế rồi ép vào bình phương 3 số