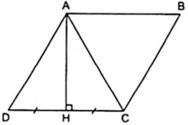
Gọi H là chân đường cao kẻ từ đỉnh A xuống cạnh CD, theo giả thiết ta có:

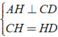 ⇒ AH là đường trung trực của đoạn CD nên AC = AD       ( 1 )

Áp dụng định nghĩa của hình thoi ABCD, ta có

AD = AB = BC = CD       ( 2 )

Từ ( 1 ) và ( 2 ) ta có AD = AC = CD ⇒ Δ ACD là tam giác đều

.

Chọn D

Chu vi hình thoi bằng 16(cm) nên độ dài một cạnh bằng:

16 : 4 = 4(cm)

Gọi M là trung điểm của AD.

*Trong tam giác vuông AHD ta có HM là trung tuyến thuộc cạnh huyền, suy ra: HM = AM = 1/2 AD = 1/2 . 4 = 2(cm)

⇒ AM = HM = AH = 2cm

⇒ ∆ AHM đều

⇒ ∠ (HAM ) = 60 0

*Trong tam giác vuông AHD, ta có:

∠ (HAD) +  ∠ D =  90 0

⇒  ∠ D =  90 0 -  ∠ (HAD) =  90 0  –  60 0  =  30 0

⇒  ∠ B =  ∠ D =  30 0  ( t/chất hình thoi)

        ∠ B +  ∠ C =  180 0  ( hai góc trong cùng phía bù nhau)

⇒ ∠ C =  180 0 -  ∠ B =  180 0  –  30 0  =  150 0

⇒  ∠ A =  ∠ C =  150 0  ( tính chất hình thoi).

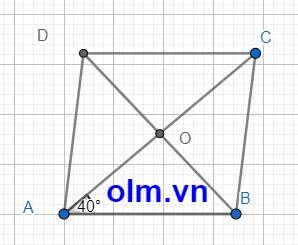
Vì ABCD  là hình thoi nên ⇒ tam giác ABD cân tại A

Vì O là trung điểm DB nên AO là truyến là đường phân giác của tam giác ABD

⇒ \(\widehat{DAO}\) = 40⁰

⇒ \(\widehat{DAB}\) = 40⁰ + 40⁰ = 180⁰

⇒ \(\widehat{ADC}\) = 180⁰ - 80⁰ = 100⁰

⇒ \(\widehat{DCB}\) = 180⁰ - 100⁰ = 80⁰

\(\Rightarrow\) \(\widehat{ABC}\) = 180⁰ - 80⁰ = 100⁰