Cho tam giác ABC cân tại A. các điểm D,E theo thứ tự chuyển động trên các cạnh AB; AC sao cho AD = DE. Trung điểm I của DE chuyển động trên đương thẳng nào? Mn giúp mk vs mk đang cần gấp lắm!!! 😭 ai làm dùm mk sẽ tik cho 😊

Những câu hỏi liên quan
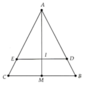
Cho tam giác ABC cân tại A. Các điểm D, E theo thứ tự chuyển động trên cạnh AB, AC sao cho AD = AE. Trung điểm I của đoạn thẳng DE di chuyển trên đường nào?
Tương tự 2A.
Cho D º B, E º C Þ Vị trí điểm I.
CHo D º A, E º A Þ Vị trí điểm I.
Kết luận: I thuộc trung trực của BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A các điểm E và D theo thứ tự di chuyển trên hai cạnh AB và AC sao cho AD = CE. CMR: các đường trung trực của DE luôn đi qua 1 điểm cố định
cho tam giác ABC cân tại A. Các điểm E và D theo thứ tự di chuyển trên 2 cạnh AB và AD sao cho AD=CE. Chứng minh rằng các đường trung trực của DE luôn đi qua 1 điểm cố định
cho tam giác abc cân tại a trên các cạnh bên ab ac lấy theo thứ tự các điểm d và e sao cho ad=ae
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.
chứng minh BE=CD
Có: \(\left\{{}\begin{matrix}AD+BD=AB\\AE+EC=AC\end{matrix}\right.\)
Mà: \(\left\{{}\begin{matrix}AD=AE\left(GT\right)\\AB=AC\left(GT\right)\end{matrix}\right.\)
=> BD = EC
Xét ΔBDC và ΔCEB ta có :
BD = EC (cmt)
Góc DBC = Góc ECB (GT)
BC: cạnh chung
=> ΔBDC = ΔCEB (c - g - c)
=> CD = BE (2 cạnh tuwowg ứng)
Đúng 0
Bình luận (2)
Cho tam giác ABC cân tại A. Các điểm M, N theo thứ tự chuyển động trên các cạnh AB, AC sao cho AM = CN. a) Chứng minh đường tròn ngoại tiếp tam giác AMN luôn đi qua một điểm cố định khác A. b) Tìm quỹ tích tâm đường tròn ngoại tiếp tam giác AMN
ai trả lời được mình xin hậu tạ thẻ 10k
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD=AE
Biết góc A=50độ Số đo góc D của tứ giác BDEC là...
Trong tam giác AD1E, có AD = AE(gt) nên tam giác AD1E là tam giác cân tại A
mà Â =50o => góc AD1E = \(\frac{180^0-Â}{2}=\frac{180^0-50^0}{2}=\frac{130^0}{2}=65^0\)(1)
Tam giác ABC cân tại A=> góc ABC \(=\frac{180^0-Â}{2}=\frac{180^0-50^0}{2}=\frac{130^0}{2}=65^0\)(2)
Từ (1), (2) => góc AD1E = ABC nên tứ giác BDEC là hình thang (ở vị trí đ/vị)
mà góc D1 +D2 =1800 ( kề bù), do đó D2 = 1800 - D1 = 1800 - 650 = 1150
Vậy góc D trong tứ giác BDEC = 1150
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng góc A = 50o.
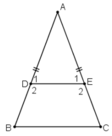
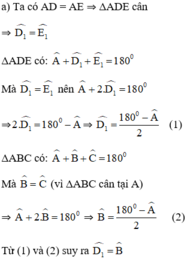
Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
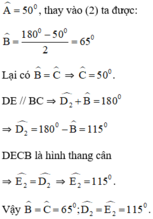
Đúng 0
Bình luận (0)
Cho tam giác vuông cân ABC cố định, M chuyển động trên cạnh huyền BC. Đường thẳng qua M và vuông góc với BC cắt các đường thẳng BC, CA theo thứ tự tại D và E. Gọi I là trung điểm của CE, K là trung điểm của BD, O là rug điểm của IK. Khi M chuyển động trên BC thì O chuyển động trên dường nào.













