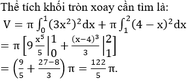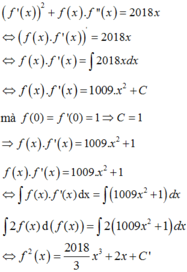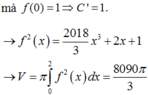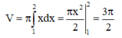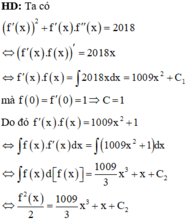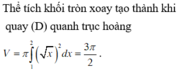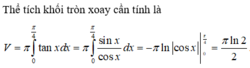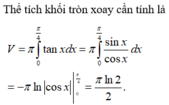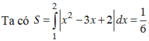Cho hình phẳng giới hạn bởi đồ thị hàm số f(x) = \(\sin\dfrac{x}{2}\), trục hoành và hai đường thẳng x = 0, \(x=\dfrac{\pi}{2}\). Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox.

Những câu hỏi liên quan
Cho hàm số
y
f
(
x
)
3
x
2
khi
x
≤
1...
Đọc tiếp
Cho hàm số y = f ( x ) = 3 x 2 khi x ≤ 1 4 - x khi > 1 . Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và các đường thẳng x = 0, x = 2 quanh trục hoành bằng
A. 29 4
B. 29 π 4
C. 122 15
D. 122 π 15
Cho hàm số f(x) thỏa mãn
f
x
2
+
f
x
.
f
x
2018
x
∀
x
∈
R
và f(0) f’(0) 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x 0; x 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục...
Đọc tiếp
Cho hàm số f(x) thỏa mãn f ' x 2 + f x . f " x = 2018 x ∀ x ∈ R và f(0) = f’(0) = 1. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0; x = 2. Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2
B. V = 4036π
C. V = 8090 3 π
D. V = 8090π/3
Cho hình phẳng (D) giới hạn bởi đồ thị hàm số
y
x
, hai đường thẳng
x
1
,
x
2
và trục hoành. Tính thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục hoành. A.
V
3
π
2
B.
V
3
π
C.
V
3...
Đọc tiếp
Cho hình phẳng (D) giới hạn bởi đồ thị hàm số y = x , hai đường thẳng x = 1 , x = 2 và trục hoành. Tính thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục hoành.
A. V = 3 π 2
B. V = 3 π
C. V = 3 2
D. V = 2 π 3
Cho hàm số f(x) thỏa mãn
f
x
2
+
f
x
f
x
2018
x
,
∀
x
∈
ℝ
và
f
0
f
0
1
. Gọi (H) là hình phẳng giới hạn bởi đồ th...
Đọc tiếp
Cho hàm số f(x) thỏa mãn f ' x 2 + f x f ' ' x = 2018 x , ∀ x ∈ ℝ và f 0 = f ' 0 = 1 . Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số f(x), trục hoành và hai đường thẳng x = 0 , x = 2 . Tính thể tích V của khối tròn xoay tạo thành khi quay (H) quanh trục Ox.
A. V = 8090 3 2 π
B. V = 4036 π
C. V = 8090 3 π
D. V = 8090 3 π
Cho miền phẳng (D) giới hạn bởi đồ thị hàm số
y
x
,
hai đường thẳng
x
1
,
x
2
và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay (D) quanh trục hoành. A.
3
π
2
B.
3
π
C.
3...
Đọc tiếp
Cho miền phẳng (D) giới hạn bởi đồ thị hàm số y = x , hai đường thẳng x = 1 , x = 2 và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay (D) quanh trục hoành.
A. 3 π 2
B. 3 π
C. 3 2
D. 2 π 3
Đáp án D
V = π ∫ a b y 2 d x = π ∫ 1 2 x d x = π x 2 2 1 2 = 3 π 2
Đúng 0
Bình luận (0)
Cho miền phẳng (D) giới hạn bởi đồ thị hàm số
y
x
, hai đường thẳng x 1, x 2 và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay (D) quanh trục hoành. A.
3
π
2
B. 3π C.
3
2
D.
2
π
3
Đọc tiếp
Cho miền phẳng (D) giới hạn bởi đồ thị hàm số y = x , hai đường thẳng x = 1, x = 2 và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay (D) quanh trục hoành.
A. 3 π 2
B. 3π
C. 3 2
D. 2 π 3
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y
tan
x
, trục hoành và các đường thẳng x 0, x
π
4
quanh trục hoành là A. V
π
4
B. V
πln
2
2
C. V
π
2
4...
Đọc tiếp
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng
giới hạn bởi đồ thị hàm số y = tan x , trục hoành và các
đường thẳng x = 0, x= π 4 quanh trục hoành là
A. V= π 4
B. V = πln 2 2
C. V = π 2 4
D. V = π 4
Cho hàm số y f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y f(x) trục hoành và hai đường thẳng x a; xn Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x =a; x=n Thể tích của khối của khối tròn xoay tạo thành khi quay D quanh trục hoành được tính theo công thức:

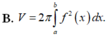
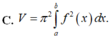
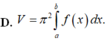
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số
y
tan
x
trục hoành và các đường thẳng
x
0
,
x
π
4
quanh trục hoành là A.
V
π
4
B.
V
π...
Đọc tiếp
Thể tích của khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số y = tan x trục hoành và các đường thẳng x = 0 , x = π 4 quanh trục hoành là
A. V = π 4
B. V = π ln 2 2
C. V = π 2 4
D. V = π 4
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số
y
x
2
-
3
x
+
2
trục hoành và hai đường thẳng x1,x2 Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành bằng A. π/30 B. π/6 C. 1/6 D. 1/30
Đọc tiếp
Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = x 2 - 3 x + 2 trục hoành và hai đường thẳng x=1,x=2 Thể tích của khối tròn xoay tạo thành khi quay D quanh trục hoành bằng
A. π/30
B. π/6
C. 1/6
D. 1/30