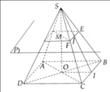
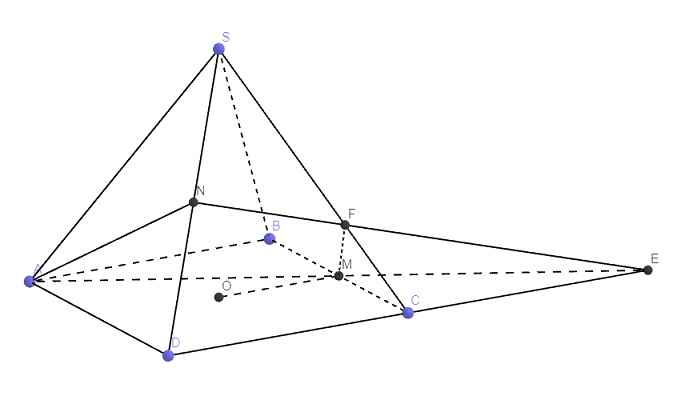
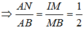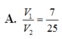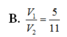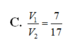Cho khối chóp cụt đều tạo bởi khối chóp đỉnh S, diện tích hai đáy lần lượt là B, B' và chiều cao h. Chọn trục Ox chứa đường cao của khối chóp và gốc O trùng với đỉnh S (Hình 21). Hai mặt phẳng đáy của khối chóp cụt đều lần lượt cắt Ox tại I và I'.
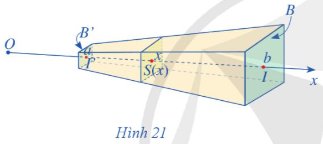
Đặt OI = b, OI' = a (a < b). Một mặt phẳng (P) vuông góc với trục Ox tại x (a ≤ x ≤ b), cắt khối chóp cụt đều theo hình phẳng có diện tích S(x). Người ta chứng minh rằng S(x) = \(B\dfrac{x^2}{b^2}\). Tính thể tích khối chóp cụt đều đó.