Giải hệ phương trình sau:
{2x+y=55x+2y=12{2x+y=55x+2y=12
Đáp án: x = và y =
Giải hệ phương trình sau:
{2x+y=55x+2y=12{2x+y=55x+2y=12
Đáp án: x =............. và y = ...............
thôi, giơ hai tay nói CHỊU
Giải các hệ phương trình sau bằng phương pháp thế: 3 x - y = 5 5 x + 2 y = 23
Cách 1
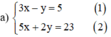
Từ (1) ta rút ra được y = 3x – 5 (*)
Thế (*) vào phương trình (2) ta được :
5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.
Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.
Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).
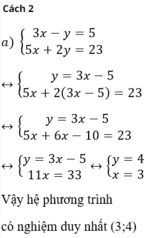
Giải các hệ phương trình sau bằng phương pháp thế:
a ) 3 x − y = 5 5 x + 2 y = 23 b ) 3 x + 5 y = 1 2 x − y = − 8 c ) x y = 2 3 x + y − 10 = 0
Cách 1
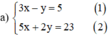
Từ (1) ta rút ra được y = 3x – 5 (*)
Thế (*) vào phương trình (2) ta được :
5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.
Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.
Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).
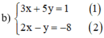
Từ (2) ta rút ra được y = 2x + 8 (*)
Thế (*) vào phương trình (1) ta được :
3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.
Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.
Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).
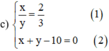
Từ (1) ta rút ra được x = 2 3 y (*)
Thế (*) vào phương trình (2) ta được :
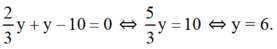
Thay y = 6 vào (*) ta được x = 4.
Vậy hệ phương trình có nghiệm duy nhất (x ; y) = (4 ; 6).
Cách 2

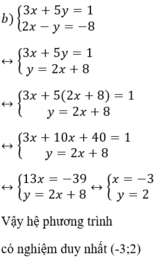
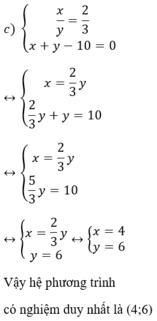
Kiến thức áp dụng
+ Giải hệ phương trình 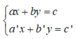 ta làm như sau:
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.
Cho hệ phương trình:\(\left\{{}\begin{matrix}2x+y=5m-1\\x-2y=2\end{matrix}\right.\)(m là tham số)
1.Giải hệ phương trình với m=1
2.Tìm m để hệ phương trình có nghiệm (x;y) thỏa mãn đẳng thức \(x^2+2y^2=2\)
Linh tinh đếyyy ạ. Có gì sai thông cảm nhaaaa
Giải hệ phương trình: 2x + 1/y = 3/x và 2y + 1/x = 3/y
Đề bài là \(\left\{{}\begin{matrix}2x+\dfrac{1}{y}=\dfrac{3}{x}\\2y+\dfrac{1}{x}=\dfrac{3}{y}\end{matrix}\right.\) hay \(\left\{{}\begin{matrix}\dfrac{2x+1}{y}=\dfrac{3}{x}\\\dfrac{2y+1}{x}=\dfrac{3}{y}\end{matrix}\right.\) nhỉ?
Tốt nhất là bạn sử dụng tính năng gõ công thức trực quan, rất dễ sử dụng, nó nằm chỗ khoanh đỏ này trong khung soạn thảo:

Click vô đó, rồi chọn

Hệ 2 ẩn nằm ở đầu tiên hàng 2
Phân thức thì chỉ cần gõ "/" hoặc chọn biểu tượng phân thức

Giải hệ phương trình sau: \(\left\{{}\begin{matrix}x^3=2x+y\\y^3=2y+x\end{matrix}\right.\)
Lời giải:
Lấy 2 PT trừ theo vế thì:
$x^3-y^3=x-y$
$\Leftrightarrow (x-y)(x^2+xy+y^2)-(x-y)=0$
$\Leftrightarrow (x-y)(x^2+xy+y^2-1)=0$
$\Rightarrow x-y=0$ hoặc $x^2+xy+y^2=1$
TH1: $x-y=0\Leftrightarrow x=y$
Thay vào PT(1):
$x^3=3x\Leftrightarrow x(x^2-3)=0\Leftrightarrow x=0$ hoặc $x=\pm \sqrt{3}$
Vậy $(x,y)=(0,0), (\sqrt{3}, \sqrt{3}), (-\sqrt{3}, -\sqrt{3})$
TH2: $x^2+xy+y^2=1(*)$
Cộng 2 PT theo vế: $x^3+y^3=3(x+y)$
$\Leftrightarrow (x+y)(x^2-xy+y^2-3)=0$
Nếu $x+y=0$ thì $x=-y$. Thay vào $(*)$:
$x^2+x(-x)+y^2=1$
$\Leftrightarrow y^2=1\Leftrightarrow y=\pm 1$
Vậy $(x,y)=(1,-1), (-1,1)$
Nếu $x^2-xy+y^2-3=0$
$\Leftrightarrow (x^2+xy+y^2)-2xy-3=0$
$\Leftrightarrow 1-2xy-3=0$
$\Leftrightarrow xy=-1$
$x^2+y^2=1-xy=1-(-1)=2$
$\Leftrightarrow (x+y)^2-2xy=2$
$\Leftrightarrow (x+y)^2-2(-1)=2$
$\Leftrightarrow x+y=0$
$\Leftrightarrow x=-y$. Thay vào $xy=-1$ thì: $y^2=1\Leftrightarrow y=\pm 1$
Nếu $y=1$ thì $x=-y=-1$. Nếu $y=-1$ thì $x=-y=1$
Vậy $(x,y)=(-1,1), (1,-1)$.
Vậy............
Giải hệ phương trình sau:
\(\hept{\begin{cases}2x+y=5\\5x+2y=12\end{cases}}\)
Tìm x ; y
\(\Leftrightarrow\hept{\begin{cases}y=5-2x\\5x+2.\left(5-2x\right)=12\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=5-2x\\5x+10-4x=12\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=5-2x\\x=12-10\end{cases}\Leftrightarrow\hept{\begin{cases}y=5-2.2=1\\x=2\end{cases}}}\)
\(\hept{\begin{cases}2x+y=5\\5x+2y=12\end{cases}\Leftrightarrow\hept{\begin{cases}4x+2y=10\\5x+2y=12\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}-x=-2\\4x+2y=10\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=1\end{cases}}\)
Giải phương trình và hệ phương trình sau :
a ) \(\sqrt{x+1}+2x\sqrt{x+3}=2x+\sqrt{x^2+4x+3}\)
b) \(\hept{\begin{cases}x+y^2=x^3\\y+x^2=y^3\end{cases}}\)
c) \(\hept{\begin{cases}x^2+y^2-4x+2y=-3\\x^2+y^2-xy+x-2y=12\end{cases}}\)
1) Ta có pt \(\Leftrightarrow\sqrt{x+1}+2x\sqrt{x+3}=2x+\sqrt{\left(x+1\right)\left(x+3\right)}\)
Đặt \(\sqrt{x+1}=a;\sqrt{x+3}=b\left(b>a\ge0\right)\)
Ta có pt \(\Leftrightarrow a+2xb=2x+ab\Leftrightarrow a\left(1-b\right)-2x\left(1-b\right)=0\Leftrightarrow\left(a-2x\right)\left(1-b\right)=0\)
Đến đây tự thay a,b vào rồi giải pt bậc 2 nhá !
b, trừ từng vế của 2 pt trong hệ ta có pt hệ quả có nhân tử chung là x-y
Giải hệ phương trình \(\hept{\begin{cases}\frac{3+2x-y}{2x-y}-\frac{6}{x+y}=0\\\frac{1-4x+2y}{2x-y}-\frac{1+2x+2y}{x+y}=0\end{cases}}\)
Hint: đặt \(\frac{1}{2x-y}=a;\frac{1}{x+y}=b\)