Cho tứ giác AMNB có góc AMN= góc BNM.
Chứng minh A,M,N,B thuộc một đường tròn
Những câu hỏi liên quan
Cho tam giác ABC nhọn . AM và BN là hai đường cao của tam giác ( M thuộc BC , N thuộc AC ) a) chứng minh tứ giác ANMB nội tiếp đường tròn b) chứng minh góc AMN = góc ABN c) giả sử góc C = 30°. Tính số đo cung MN
a) xét tứ giác ANMB có góc ANB = góc AMB lại cùng nhìn cạnh AB nên theo cung chứa góc thì tứ giác ANMB nội tiếp
b) có tứ giác ANMB nội tiếp nên góc AMN = góc ABN ( 2 góc nội tiếp cùng chắn cung AN của đường tròn (ANMB)
c) ta có tam giác AMC vuông tại M
góc C = 30 độ thì góc MAC = 60 độ và là góc nội tiếp chắn cung MN
=> góc MAC = 1/2 số đo cung MN
=> số đo cung MN = 2.góc MAC = 2.60 = 120 độ
vậy cung MN = 120 độ
Đúng 0
Bình luận (0)
cho nửa đường tròn (o;r) đường kính AB. Gọi Ax, By là các tia vuông góc với AB(Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi D là điểm bất kì thuộc nửa đường tròn.Tiếp tuyến tại D cắt Ax, By theo thứ tự tại M và N.a) Tứ giác AMNB là hình gì?b) Tính số đo góc MÔN.c) Chứng minh: MNAM+BN.d)Chứng minh: AMxBNR2.e)Đường tròn , đường kính MN tiếp xúc với AB tại 0.g) tìm vị trí của D để tứ giác AMNB có chu vi nhỏ nhất.
Đọc tiếp
cho nửa đường tròn (o;r) đường kính AB. Gọi Ax, By là các tia vuông góc với AB(Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi D là điểm bất kì thuộc nửa đường tròn.Tiếp tuyến tại D cắt Ax, By theo thứ tự tại M và N.
a) Tứ giác AMNB là hình gì?
b) Tính số đo góc MÔN.
c) Chứng minh: MN=AM+BN.
d)Chứng minh: AMxBN=R2.
e)Đường tròn , đường kính MN tiếp xúc với AB tại 0.
g) tìm vị trí của D để tứ giác AMNB có chu vi nhỏ nhất.
cho tam giác ABC vuông tại A. Vẽ các đường tròn O và i đi qua A và tiếp xúc với BC tại các điểm B và C. Gọi M là trung điểm của BC. Chứng Minh
a) Các đường tròn O và i tiếp xúc với nhau
b) AM là tiếp tuyến chung của hai đường tròn O và i
c) tam giác OMI vuông
d) BC là tiếp tuyến của đường tròn ngoại tiếp tam giác OMI.
Đúng 0
Bình luận (0)
1) Cho hình bình hành ABCD có góc A lớn hơn 90 độ. Từ A vẽ AM và AN thẳng góc BC và CD ( M thuộc BC và N thuộc CD )
a) Chứng minh tam giác ABC đồng dạng tam giác AMN.
b) Tính các góc của hình bình hành ABCD biết diện tích tam giác AMN = 1/8 diện tích tứ giác ABCD.
c) Chúng minh 4 điểm A, C, M, N cùng thuộc 1 đường tròn.
1. Cho đường tròn ( 0; R) đường kính BC, Điểm A thuộc đường tròn. hạ AH vuông góc BC; HE vuông góc AB; HF vuông góc AC. Đường thẳng EF cắt Đường tròn tại M, N.a Chứng minh tứ giác AEHF là hình chữ nhậtb. Chứng minh AE. AB A F . ACc. Chứng minh tam giác AMN când. Cho BC cố định điểm A chuyển động trên cung lớn BC. Chứng minh đường tròn tâm (A. AM) luôn tiếp xúc với một đường thẳng cố định.2.
Đọc tiếp
1. Cho đường tròn ( 0; R) đường kính BC, Điểm A thuộc đường tròn. hạ AH vuông góc BC; HE vuông góc AB; HF vuông góc AC. Đường thẳng EF cắt Đường tròn tại M, N.
a Chứng minh tứ giác AEHF là hình chữ nhật
b. Chứng minh AE. AB = A F . AC
c. Chứng minh tam giác AMN cân
d. Cho BC cố định điểm A chuyển động trên cung lớn BC. Chứng minh đường tròn tâm (A. AM) luôn tiếp xúc với một đường thẳng cố định.
2.
cho nửa đường tròn đường kính AB và C, D thuộc nửa đường tròn. AC, AD cắt tiếp tuyến Bx lần lượt tại E và F.
a. Cm góc ABD = góc AFB,góc ABC =góc AEB
b. Cm tứ giác CDFE nội tiếp
c. Gọi I là trung điểm của FB. Chứng minh DI là tiếp tuyến của nửa đường tròn
d. Giả sử CD cắt Bx tại G. Tia phân giác của góc CGE cắt AE và AF lần lượt tại N và M. Chứng minh tam giác AMN cân
Dễ thấy: ABCˆ=CDAˆ=BEAˆABC^=CDA^=BEA^ mà CDAˆ=NDGˆCDA^=NDG^(đối đỉnh)
=>GEMˆ=GDNˆ=>=>GEM^=GDN^=> Tam giác GDN đồng dạng vs Tam giác GEM
=>GNDˆ=GMEˆ=>AMNˆ=ANMˆ=>GND^=GME^=>AMN^=ANM^
Vậy tam giác AMN cân tại A
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) đường kính BC. Điểm A thuộc đường tròn. Hạ AH vuông góc BC, HE vuông góc AB, HF vuông góc AC. Đường thẳng EF cắt đường tròn tại M và N. Chứng minh tam giác AMN cân tại A.
Cho tam giác ABC có ba góc nhọn nói tiếp đường tròn tâm (O) về hai đường cao BE và CF a. Chứng minh tứ giác B FEC nói tiếp đường tròn. b. Chứng minh góc AFE=góc ACB b. Chứng minh AO thuộc EF
Cho đường tròn (O; R) đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến d và d với (O). Một đường thẳng qua O cắt d ở M và cắt d ở P. Từ O vẽ một tia vuông góc với MP và cắt d ở Na, Chứng minh OM OP và tam giác NMP cânb, Gọi I là hình chiếu vuông góc của O lên MN. Chứng minh OI R và MN là tiếp tuyến của (O)c, Chứng minh AM. BN
R
2
d, Tìm vị trí của M để tứ giác AMNB có diện tích đạt giá trị nhỏ nhất
Đọc tiếp
Cho đường tròn (O; R) đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến d và d' với (O). Một đường thẳng qua O cắt d ở M và cắt d' ở P. Từ O vẽ một tia vuông góc với MP và cắt d' ở N
a, Chứng minh OM = OP và tam giác NMP cân
b, Gọi I là hình chiếu vuông góc của O lên MN. Chứng minh OI = R và MN là tiếp tuyến của (O)
c, Chứng minh AM. BN = R 2
d, Tìm vị trí của M để tứ giác AMNB có diện tích đạt giá trị nhỏ nhất
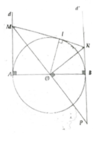
a, ∆MAO = ∆PBO => MO = OP => ∆MNP cân
Vì đường cao NO đồng thời là đường trung tuyến
b, 1 O I 2 - 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => OI = R
=> MN là tiếp tuyến của (O)
c, AM.BN = MI.IN = O I 2 = R 2
d, S A M N B = M N . A B 2
=> S A M N B min
<=> M N m i n <=> AM = R
Đúng 0
Bình luận (0)
Cho đường tròn (O;R), đường kín AB. Qua A và B vẽ lần lượt 2 tiếp tuyến (d) và (d) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d) ở P. Từ O vẽ một tia vuông góc với MP và cắt đường thẳng (d) ở Na/ Chứng minh OM OP và tam giác ANP cânb/ Vẽ OI vuông góc với MN. Chứng minh OI R và MN là tiếp tuyến của đường tròn (O)c/ Chứng minh AM.BN R2d/ Tìm vị tró của M để diện tích tứ giác AMNB nhỏ nhất. Vẽ hình minh họa!
Đọc tiếp
Cho đường tròn (O;R), đường kín AB. Qua A và B vẽ lần lượt 2 tiếp tuyến (d) và (d') với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d') ở P. Từ O vẽ một tia vuông góc với MP và cắt đường thẳng (d') ở N
a/ Chứng minh OM = OP và tam giác ANP cân
b/ Vẽ OI vuông góc với MN. Chứng minh OI = R và MN là tiếp tuyến của đường tròn (O)
c/ Chứng minh AM.BN = R2
d/ Tìm vị tró của M để diện tích tứ giác AMNB nhỏ nhất. Vẽ hình minh họa!