bằng cách đặt u và dv

Bằng cách đặt u = ln x , d v = x 2 d x thì tích phân ∫ 1 2 x 2 ln x d x biến đổi thành kết quả nào sau đây?
A. x 3 ln x 3 1 3 − 1 3 ∫ 1 3 x 2 d x
B. x 2 ln x 2 1 3 − 1 3 ∫ 1 3 x 2 d x
C. x 3 ln x 3 1 3 + 1 3 ∫ 1 3 x 2 d x
D. − x 3 ln x 3 1 3 − 1 3 ∫ 1 3 x 2 d x
Đáp án A
Ta có: ∫ 1 2 x 2 ln x d x = 1 3 ∫ 1 2 ln x d x 3 = x 3 ln x 3 1 3 − 1 3 ∫ 1 3 x 2 d x
Tính tích phân I=\(\int\limits^{\pi}_0\)\(x^2cos2xdx\) bằng cách đặt \(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\).Mệnh đề nào dưới đây đúng?
A. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-\int\limits^{\pi}_0xsin2xdx\)
B. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-2\int\limits^{\pi}_0xsin2xdx\)
C. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+\int\limits^{\pi}_0xsin2xdx\)
D. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+2\int\limits^{\pi}_0xsin2xdx\)
\(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2xdx\\v=\dfrac{1}{2}sin2x\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{2}x^2sin2x|^{\pi}_0-\int\limits^{\pi}_0x.sin2xdx\)
Tính I = ∫ x s inx d x , đặt u = x , d v = s inx dx . Khi đó I biến đổi thành
A. I = − x c osx- ∫ c osx d x
B. I = − x c osx + ∫ c osx d x ,
C. I = x c osx + ∫ c osx d x ,
D. I = − x sin x + ∫ c osx d x
Đáp án B
Ta có u = x d v = sin x d x ⇒ d u = d x v = − c o s x
Khi đó I = − x c osx + ∫ c osx d x ,
Bằng cách đặt ẩn phụ theo hướng dẫn, giải các phương trình sau: 2 + 2 x 2 - 1 = 2 x 2 - 2
Hướng dẫn: Đặt u = x 2 - 1.
Nếu đặt u = x 2 − 1 thì x 2 = u + 1 nên phương trình có dạng
( 2 + 2)u = 2(u + 1) − 2 (1)
Ta giải phương trình (1):
(1) ⇔ 2 u + 2u = 2u + 2 − 2
⇔ 2 u = 2 − 2
⇔ 2 u = 2 ( 2 − 1) ⇔ u = 2 − 1
⇔ x 2 − 1 = 2 − 1
⇔ x 2 = 2
⇔ x = 1
Tính tích phân I = ∫ 0 π x 2 cos 2 2 xdx bằng cách đặt u = x 2 d v = cos 2 x dx . Mệnh đề nào dưới đây đúng?
A. I = 1 2 x 2 sin 2 x 0 π - ∫ 0 π x sin 2 xdx
B. I = 1 2 x 2 sin 2 x 0 π - 2 ∫ 0 π x sin 2 xdx
C. I = 1 2 x 2 sin 2 x 0 π + 2 ∫ 0 π x sin 2 xdx
D. I = 1 2 x 2 sin 2 x 0 π + ∫ 0 π x sin 2 xdx
Tính tích phân I = ∫ 0 π x 2 c o s 2 2 x d x bằng cách đặt u = x 2 d v = c o s 2 x d x . Mệnh đề nào dưới đây đúng?
A. I = 1 2 x 2 sin 2 x π 0 − ∫ 0 π x sin 2 x d x .
B. I = 1 2 x 2 sin 2 x π 0 − 2 ∫ 0 π x sin 2 x d x .
C. I = 1 2 x 2 sin 2 x π 0 + 2 ∫ 0 π x sin 2 x d x .
D. I = 1 2 x 2 sin 2 x π 0 + ∫ 0 π x sin 2 x d x .
Đáp án A.
u = x 2 d v = c o s 2 x d x ⇒ d u = 2 x d x v = 1 2 sin 2 x ⇒ I = 1 2 x 2 sin 2 x π 0 − ∫ 0 π x sin 2 x d x .
Tính tích phân I = ∫ 0 π x 2 cos 2 2 x d x bằng cách đặt u = x 2 d v = cos 2 x d x
Mệnh đề nào dưới đây đúng?
A. I = 1 2 x 2 sin 2 x 0 π - ∫ 0 π x sin 2 x d x
B. I = 1 2 x 2 sin 2 x 0 π - 2 ∫ 0 π x sin 2 x d x
C. I = 1 2 x 2 sin 2 x 0 π + 2 ∫ 0 π x sin 2 x d x
D. I = 1 2 x 2 sin 2 x 0 π + ∫ 0 π x sin 2 x d x
Cho tích phân I = ∫ 0 1 2 x + 1 2 d x
1. Tính I bằng cách khai triển 2 x + 1 2 .
2. Đặt u = 2x + 1. Biến đổi biểu thức 2 x + 1 2 dx thành g(u)du.
3. Tính ∫ u 0 u 1 g u d u và so sánh kết quả với I trong câu 1
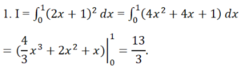
2. Vì u = 2x+1 nên du = 2dx. Ta có 2 x + 1 2 d x = u 2 d u 2

Bằng cách đặt u = a – b, v = a + b, hãy biến đổi cosu + cosv, sinu + sinv thành tích.
Khi tính nguyên hàm ∫ x - 3 x + 1 d x , bằng cách đặt u = x + 1 ta được nguyên hàm nào?
A. ∫ 2 u u 2 - 4 d u
B. ∫ u 2 - 4 d u
C. ∫ 2 u 2 - 4 d u
D. ∫ u 2 - 3 d u