So sánh hai số sau , số nào lớnhon:
B=x-y/x+y và x^2-y^2/x^2+y^2 voi x>y>0
So sánh hai phân thức sau: \(\frac{x-y}{x+y}\) và \(\frac{x^2-y^2}{x^2+y^2}\) với x > 0, y > 0
Có thể thế vào: x=2;y=1.Ta có:
\(\frac{x-y}{x+y}=\frac{2-1}{2+1}=\frac{1}{3}\) và \(\frac{x^2-y^2}{x^2+y^2}=\frac{2^2-1^2}{2^2+1^2}=\frac{3}{5}\)
\(\Rightarrow\frac{1}{3}< \frac{3}{5}\Rightarrow\frac{x-y}{x+y}< \frac{x^2-y^2}{x^2+y^2}\)
cái này mik giải để giúp mọi người nếu bạn cho rằng sai thì giải thử xem.
Cách này thì thi viết:
Ta có: \(\frac{x^2-y^2}{x^2+y^2}=\frac{\left(x+y\right)\left(x-y\right)}{\left(x+y\right)^2-2xy}\left(1\right)\)
\(\frac{x-y}{x+y}=\frac{\left(x-y\right)\left(x+y\right)}{\left(x+y\right)^2}\left(2\right)\)
\(\Rightarrow\left(x+y\right)^2-2xy< \left(x+y\right)^2\)\(\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\Rightarrow\frac{x-y}{x+y}< \frac{x^2-y^2}{x^2+y^2}\)
tim hai so x va y biet x^2+y^2;x^2-y^2 va x^2.y^2 ti le nghich voi 1/25,1/7 va 1/576(x khac 0 va y khac 0)
cho x>y>0 hãy so sánh A=x-y/x+y và B=x^2-y^2/x^2+y^2
Ta có: \(A=\dfrac{x-y}{x+y}\)
\(=\dfrac{\left(x-y\right)\left(x+y\right)}{\left(x+y\right)^2}\)
\(=\dfrac{x^2-y^2}{x^2+2xy+y^2}\)
Ta có: \(x^2+2xy+y^2>x^2+y^2\forall x>y>0\)
\(\Leftrightarrow\dfrac{x^2-y^2}{x^2+2xy+y^2}< \dfrac{x^2-y^2}{x^2+y^2}\)
hay A<B
1: So sánh hai số - 0,162000 và -0,(162)
2: Biết hai đại lượng x và y tỷ lệ nghịch với nhau và khi x= -3 thì y = -6. Hỏi khi x = 9 thì y bằng bao nhiêu?
3Hai đại lượng x và y tỉ lệ thuận với nhau và khi x = – 6 thì y = 3. Nếu x = 20 thì y =?
c1: -0,162000>-0,(162)
c2: y=2
c3: y=-10
c4: thêm đk AC=BF
So sánh x-y/x+y và x^2-y^2/x^2+xy+y^2 Với x>y>0
Hình 11a) biểu diễn đồ thị của các hàm số (với hệ số a > 0)
y = 0,5x + 2;
y = x + 2;
y = 2x + 2.
Hình 11b) biểu diễn đồ thị của các hàm số (với hệ số a < 0):
y = -2x + 2;
y = -x + 2;
y = -0,5x + 2.
QUẢNG CÁO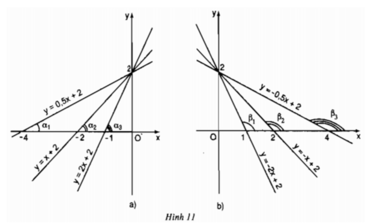
Hãy so sánh các góc α1, α2, α3 và so sánh các giá trị tương ứng của hệ số a trong các hàm số (trường hợp a > 0) rồi rút ra nhận xét.
Ta có: α1 < α2 < α3 và các giá trị tương ứng của hệ số a trong các hàm số :
0,5 < 1 < 2
Nhận xét: Khi hệ số a dương (a > 0) thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 90o
So sánh x-y/x+y và x^2-y^2/x^2+xy+y^2 với x>y>0
Ta có:\(\frac{x-y}{x+y}=\frac{\left(x-y\right)\left(x+y\right)}{\left(x+y\right)\left(x+y\right)}=\frac{x^2-y^2}{x^2+2xy+y^2}\)
Do x>y>0 =>x2+xy+y2<x2+2xy+y2
=>\(\frac{x^2-y^2}{x^2+xy+y^2}>\frac{x^2-y^2}{x^2+2xy+y^2}\)
=>\(\frac{x^2-y^2}{x^2+xy+y^2}>\frac{x-y}{x+y}\)
So sánh:(x+y)^3/x^2-y^2 và x^2-xy+y^2/x-y với x>y>0
\(\frac{\left(x+y\right)^3}{x^2-y^2}\)
\(\frac{\left(x^2-xy+y^2\right)}{x-y}=\frac{\left(x+y\right)\left(x^2-xy+y^2\right)}{\left(x+y\right)\left(x-y\right)}=\frac{x^3+y^3}{x^2-y^2}\)
Vì x > y > 0 => x^3 + y^3 < ( x+ y)^3
=> \(\frac{x^3+y^3}{x^2+y^2}\frac{x^2-xy+y^2}{x-y}\)
So sánh các số hữu tỉ x và y
a,x=1/-2 và y=-1/3
b,x=-2/3 và y=0
c,x=-0,125 và y=1,-8
d,x=-1/7 và y=-5/35
a) \(\frac{1}{-2}< \frac{-1}{3}\)
b) \(-\frac{2}{3}< 0\)
c) \(-0,125=-\frac{1}{8}=\frac{1}{-8}\)
d) \(-\frac{1}{7}=-\frac{5.1}{5.7}=-\frac{5}{35}=-\frac{5}{35}\)