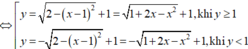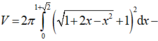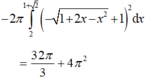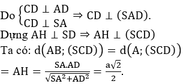Cho hình vuông ABCD cạnh bằng 1.Vẽ đường (A;R) tiếp xúc với BD.Tính bán kính R

Những câu hỏi liên quan
Bài 1 : Cho Hình Vuông ABCD có cạnh
bằng 6cm.Vẽ nửa hình tròn đường kính Ad,BC (Hình Vẽ)
Bài 2 : Cho hình vuông ABCD , có BD = 12cm và hình tròn như trên hình vẽ . Tính Diện tích hình tròn
Xem chi tiết
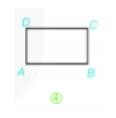
1. Vẽ hình chữ nhật ABCD có một cạnh bằng 5 cm, một cạnh bằng 3 cm theo hướng dẫn sau:Bước 1. Vẽ đoạn thẳng AB 5 cm.Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD 3 cm.Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC 3 cm.Bước 4. Nối D với C ta được hình chữ nhật ABCD.2. Em hãy kiểm tra lại hình vừa vẽ xem các cạnh đối có bằng nhau không? Các góc có bằng nhau không?
Đọc tiếp
1. Vẽ hình chữ nhật ABCD có một cạnh bằng 5 cm, một cạnh bằng 3 cm theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB = 5 cm.
Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 3 cm.
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 3 cm.
Bước 4. Nối D với C ta được hình chữ nhật ABCD.
2. Em hãy kiểm tra lại hình vừa vẽ xem các cạnh đối có bằng nhau không? Các góc có bằng nhau không?
1.
Bước 1. Vẽ đoạn thẳng AB = 5 cm.

Bước 2. Vẽ đường thẳng vuông góc với AB tại A. Trên đường thẳng đó lấy điểm D sao cho AD = 3 cm.
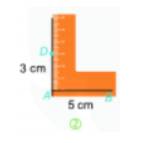
Bước 3. Vẽ đường thẳng vuông góc với AB tại B. Trên đường thẳng đó lấy điểm C sao cho BC = 3 cm.
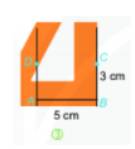
Bước 4. Nối D với C ta được hình chữ nhật ABCD.
2. Em dùng thước thẳng và thước vuông để kiểm tra
+ AB = CD ; AD = BC nên hai cạnh đối của hình chữ nhật bằng nhau
+ \(\widehat{A} = 90^0; \widehat{B} = 90^0; \widehat{C} = 90^0; \widehat{D} = 90^0\). Vậy các góc của hình chữ nhật đều bằng nhau và bằng 90o
Đúng 1
Bình luận (0)
Cho hình vuông ABCD có độ dài cạnh là 1 dm. Vẽ hai đường tròn có bán kính bằng cạnh của hình vuông có tâm lần lượt là A và C (xem hình vẽ). Hãy tính diện tích của phần gạch chéo trong hình.
Cho hình vuông ABCD có cạnh bằng a. Người ta dựng hình vuông A1B1C1D1 có cạnh bằng 1/2 đường chéo của hình vuông ABCD, dựng hình vuông A2B2C2D2 có cạnh bằng 1/2 đường chéo của hình vuông A1B1C1D1 và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích của tất cả hình vuông ABCD,A1B1C1D1,A2B2C2D2,... bằng 8 thì a bằng bao nhiêu?
Xét dãy số \(u_n=S_{A_nB_nC_nD_n}\). Ta có \(u_1=a^2\)
Ta xét hình vuông có cạnh \(x\) (diện tích là \(x^2\)). Khi đó nửa độ dài đường chéo của hình vuông này sẽ là \(\dfrac{x}{\sqrt{2}}\). Khi đó diện tích của hình vuông mới là \(\left(\dfrac{x}{\sqrt{2}}\right)^2=\dfrac{x^2}{2}\) bằng 1 nửa diện tích hình vuông ban đầu. Như vậy, ta có mối quan hệ truy hồi: \(u_{n+1}=2u_n\). Dễ thấy đây là một cấp số nhân.
Ta có \(\left(u_n\right):\left\{{}\begin{matrix}u_1=a^2\\u_{n+1}=2u_n\end{matrix}\right.\)
\(\Rightarrow S_n=\sum\limits^{\infty}_{i=1}u_i=a^2\left(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}\right)=2a^2\)
(Đẳng thức quen thuộc \(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}=2\))
Cho \(S_n=8\) \(\Rightarrow2a^2=8\Leftrightarrow a=2\).
Vậy \(a=2\) thỏa mãn ycbt.
Đúng 2
Bình luận (0)
cho hình vuông abcd có 2 đường chéo ac và bd vuông góc với nhau và bằng 12 cm, 2 đường chéo này cắt nhau tại o. từ o ta vẽ 1 hình tròn có đường kính bằng cạnh hình vuông abcd
tính diện tích hình tròn này
Trong mặt phẳng cho hình vuông ABCD cạnh
2
2
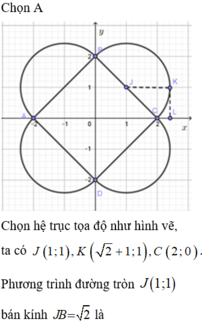
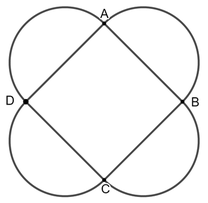
, phía ngoài hình vuông vẽ thêm bốn đường tròn nhận các cạnh của hình vuông làm đường kính (hình vẽ). Thể tích của khối tròn xoay sinh bởi hình trên khi quay quanh đường thẳng AC bằng A. B. C. D.
Đọc tiếp
Trong mặt phẳng cho hình vuông ABCD cạnh 2 2 , phía ngoài hình vuông vẽ thêm bốn đường tròn nhận các cạnh của hình vuông làm đường kính (hình vẽ). Thể tích của khối tròn xoay sinh bởi hình trên khi quay quanh đường thẳng AC bằng
A. ![]()
B. ![]()
C. ![]()
D. ![]()
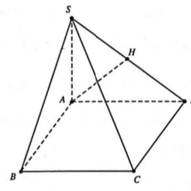
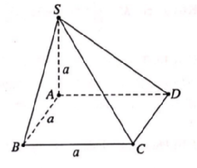
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA a (tham khảo hình vẽ). Khoảng cách từ đường thẳng AB đến mặt phẳng (SCD) bằng A.
a
2
2
. B.
a
6
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy và SA = a (tham khảo hình vẽ). Khoảng cách từ đường thẳng AB đến mặt phẳng (SCD) bằng
A. a 2 2 .
B. a 6 3 .
C. a.
D. a 3 2 .
Cho hình vuông ABCD có cạnh bằng 10cm người ta vẽ đường tròn có đường kính chính là cạnh của hình vuông. Tính diện tích phần không tô đậm
xin lỡi mình ngu nắm
Diện tích hình vuông:
10 x 10 = 100 ( c m 2 )
Bán kính hình tròn là:
10 : 2 = 5 (cm)
Diện tích hình tròn là:
5 x 5 x 3,14 = 78,5 ( c m 2 )
Diện tích phần tô màu là:
100 – 78,5 = 21,5 ( c m 2 )
Đáp số: 21,5 c m 2
s hình tròn là
5.5.3,14= 78,5 cm2
s phần ko tô là
10.10-78,5=21,5cm2
ht
Xem thêm câu trả lời
Cho hình vuông ABCD có độ dài cạnh là 1 dm. Vẽ hai đường tròn có bán kính bằng cạnh của hình vuông có tâm lần lượt là A và C. Hãy tính diện tích của phần gạch chéo trong hình.
a) Cho đoạn thẳng BC = 4cm. Vẽ tam giác đều ABC. Có thể vẽ được bao nhiêu tam giác như vậy? b) Cho BC = 4cm. Vẽ hình vuông ABCD. Có thể vẽ được bao nhiêu hình vuông như vậy? c) Vẽ hình chữ nhật có một cạnh dài 6cm; một cạnh dài 4 cm d) Vẽ hình thoi có cạnh bằng 3 cm và độ dài đường chéo bằng 6cm