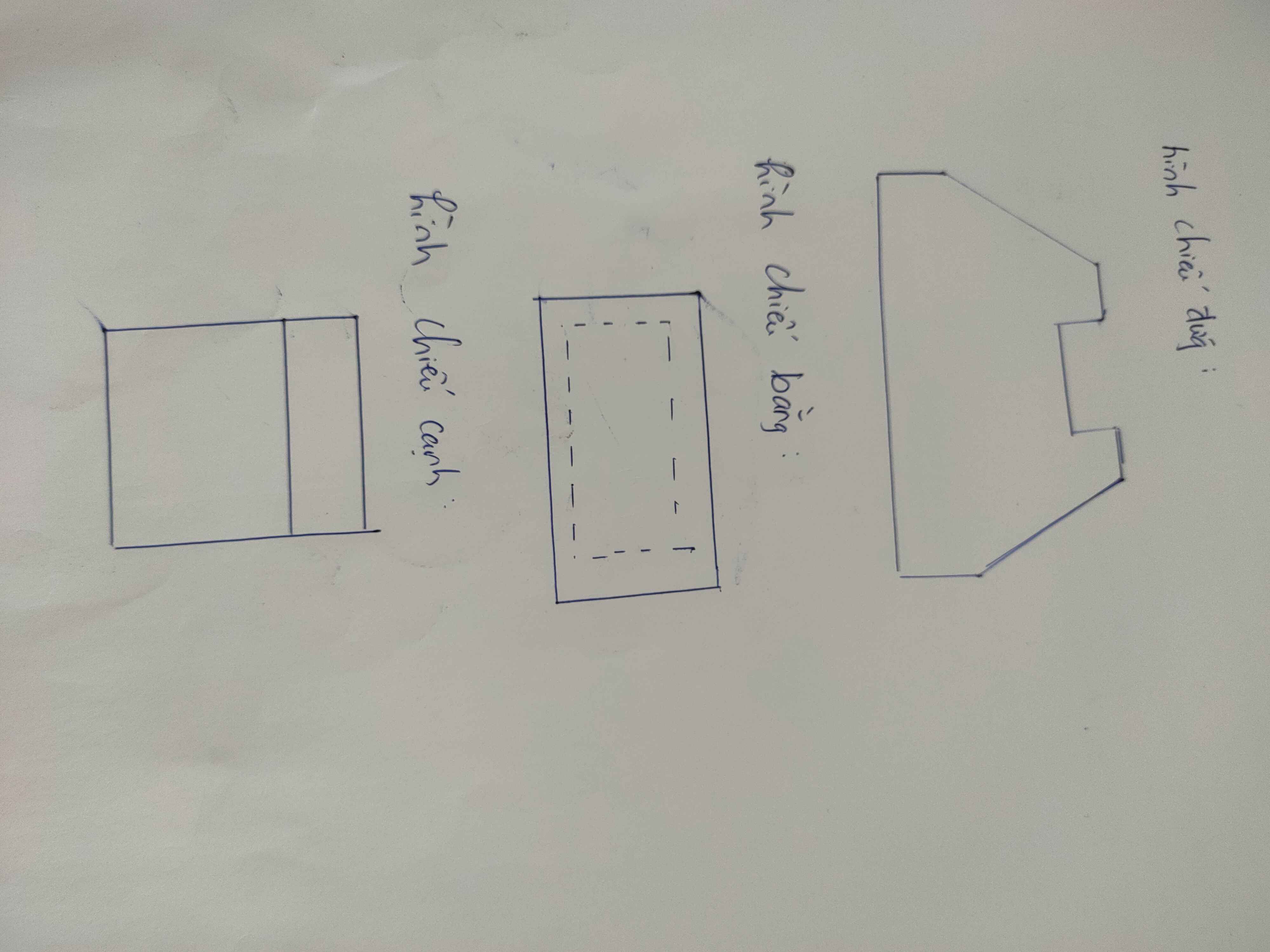
Vẽ cho e hình
Vẽ cho e hình

Những câu hỏi liên quan
Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho ∠ (EDC) = ∠ (ECD) = 15 0
Vẽ điểm F trong hình vuông sao cho ∠ (FAD) = ∠ (FDA) = 15 0 . Chứng minh rằng tam giác DEF là tam giác đều.
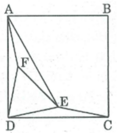
Xét ∆ EDC và ∆ FDA, tacó: ∠ (EDC) = ∠ (FDA) = 15 0
DC = AD (gt)
∠ (ECD) = ∠ (FAD) = 15 0
Suy ra: ∆ EDC = ∆ FDA (g.c.g)
⇒ DE = DF
⇒ ∆ DEF cân tại D
Lại có: ∠ (ADC) = ∠ (FDA) + ∠ (FDE) + ∠ (EDC)
⇒ ∠ (FDE) = ∠ (ADC) -( ∠ (FDA) + ∠ (EDC) )= 90 0 - ( 15 0 + 15 0 ) = 60 0
Vậy ∆ DEF đều.
Đúng 0
Bình luận (0)
Cho hình vẽ. Tập hợp E là: A. E{0;3;11;45;2020} B. E{0;3;4;11;45;2020} C. E{4;11;45;2020} D. E{0;4;11;45;2020}
Đọc tiếp
Cho hình vẽ. Tập hợp E là:
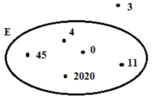
A. E={0;3;11;45;2020}
B. E={0;3;4;11;45;2020}
C. E={4;11;45;2020}
D. E={0;4;11;45;2020}
Bài 6: Cho hình vẽ: Biết . HEF = 120 Ta có, (vẽ hình giúp e ạ và vẽ hình câu c đi ạ)c) Vẽ Hm và En lần lượt là tia phân giác của GHE và HEF. Chứng minh Nm // En
Xem chi tiết
Cho hcn ABCD có dt 1575cm2. Vẽ điểm M chéo từ điểm C trên cạnh AD. Biết AM 12cm. MD 23cm. Tìm dt hình tam giác MCD
Thứ lỗi cho e vì e k biết vẽ hình trên đây ntn
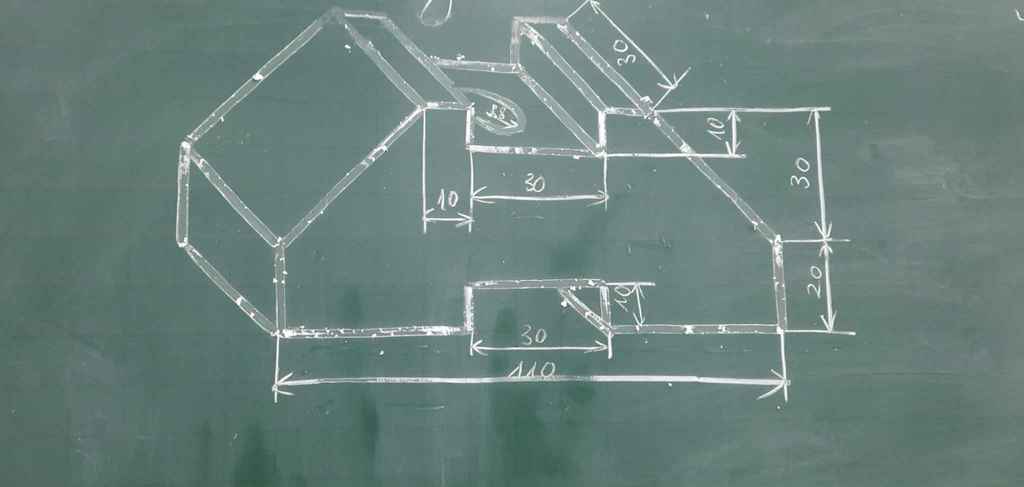
cho hình vẽ sau:
vẽ 3 hình chiếu đứng, bằng và cạnh
(mn giúp e với ạ)
Cho hình hình hành ABCD có AD 2AB. Từ C vẽ CE vuông góc với AB tại E. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE tại F, MF cắt BC tại N.a) Tứ giác MNCD là hình gì?b) Chứng minh tam giác EMC cân tại Mc) Chứng minh rằng widehat {BAD} 2widehat {AEM}Hướng dẫn:a) Chứng minh EN NC NB frac{1}{2} BCb) Chứng minh widehat {AEM} widehat {EMN} widehat {NMC} widehat {MCD} frac{1}{2}widehat {NCD}
Đọc tiếp
Cho hình hình hành \(ABCD\) có \(AD = 2AB\). Từ \(C\) vẽ \(CE\) vuông góc với \(AB\) tại \(E\). Nối \(E\) với trung điểm \(M\) của \(AD\). Từ \(M\) vẽ \(MF\) vuông góc với \(CE\) tại \(F\), \(MF\) cắt \(BC\) tại \(N\).
a) Tứ giác \(MNCD\) là hình gì?
b) Chứng minh tam giác \(EMC\) cân tại \(M\)
c) Chứng minh rằng \(\widehat {BAD} = 2\widehat {AEM}\)
Hướng dẫn:
a) Chứng minh \(EN = NC = NB = \) \(\frac{1}{2}\) \(BC\)
b) Chứng minh \(\widehat {AEM} = \widehat {EMN} = \widehat {NMC} = \widehat {MCD} = \frac{1}{2}\widehat {NCD}\)
a) Ta có:
\(MN \bot CE\) (gt)
\(AB \bot CE\) (gt)
Suy ra \(MN\) // \(AB\)
\(MN\)Mà \(AB\) // \(CD\) (do \(ABCD\) là hình bình hành) nên \(MN\)
// \(CD\)
Xét tứ giác \(MNCD\) ta có:
\(MN\) // \(CD\) (cmt)
\(MD\) // \(CN\) (do \(AD\) // \(BC\))
Suy ra \(MNCD\) là hình bình hành
Lại có:
\(AD = 2AB\) (gt);
\(AD = 2MD\) (do \(M\) là trung điểm của \(AD\))
\(AB = CD\) (do \(ABCD\) là hình bình hành)
Suy ra \(MD = CD\)
Hình bình hành \(MNCD\) có \(MD = CD\) (cmt) nên là hình thoi
b) Vì \(MNCD\) là hình thoi nên \(MD = CD = NC = MN = \frac{1}{2}AD = \frac{1}{2}BC\) (do \(AD = BD\))
Do \(NC = \frac{1}{2}BC\) nên \(N\) là trung điểm của \(BC\)
Xét \(\Delta EBC\) vuông tại \(E\) có \(EN\) là trung tuyến nên \(EN = \frac{1}{2}BC\)
Suy ra \(EN = NB = NC = \frac{1}{2}BC\)
Suy ra \(\Delta NEC\) cân tại \(N\)
Mà \(NF\) là đường cao (do \(MF \bot EC\))
Suy ra \(NF\) cũng là trung tuyến, phân giác, trung trực của \(\Delta NEC\)
Suy ra \(F\) là trung điểm \(EC\)
Xét \(\Delta MEC\) có \(MF\) là đường cao đồng thời là trung tuyến
Suy ra \(\Delta EMC\) cân tại \(M\)
c) Vì \(AB\) // \(MN\) (cmt)
Suy ra \(\widehat {{\rm{AEN}}} = \widehat {{\rm{EMN}}}\) (so le trong)
Mà \(\widehat {{\rm{EMN}}} = \widehat {{\rm{NMC}}}\) (do \(MF\) là phân giác)
\(\widehat {{\rm{NMC}}} = \widehat {{\rm{MCD}}}\) (do \(MN\) // \(CD\))
Suy ra \(\widehat {{\rm{AEM}}} = \widehat {{\rm{MCD}}}\)
Mà \(\widehat {{\rm{MCD}}} = \frac{1}{2}\widehat {{\rm{BCD}}}\) (do \(MNCD\) là hình thoi)
Và \(\widehat {{\rm{BCD}}} = \widehat {{\rm{BAD}}}\) (do \(ABCD\) là hình bình hành)
Suy ra \(\widehat {{\rm{AEM}}} = \frac{1}{2}\widehat {{\rm{BAD}}}\)
Suy ra \(\widehat {BAD} = 2\widehat {AEM}\)
Đúng 0
Bình luận (0)
Cho hình vẽ sau: Viết tập hợp D và E. A. D{m;n;p;5;10;7} và E{m,p} B. D{n;5;10;7} và E{m,p} C. D{m;n;p} và E{m,p} D. D{m;n;p;5;10;7} và E{m,n,p}
Đọc tiếp
Cho hình vẽ sau: Viết tập hợp D và E.
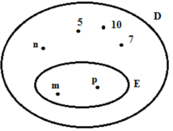
A. D={m;n;p;5;10;7} và E={m,p}
B. D={n;5;10;7} và E={m,p}
C. D={m;n;p} và E={m,p}
D. D={m;n;p;5;10;7} và E={m,n,p}
Đáp án cần chọn là: A
Ta có: D={m;n;p;5;10;7} và E={m,p}
Đúng 0
Bình luận (0)
Cho tam giác ABC, lấy điểm D trên cạnh AB, E trên cạnh AC. Hai đoạn BE, CD cắt nhau ở O, Nối D với E. Số tam giác tạo thành trong hình vẽ là ..................
Vẽ hình giúp nhé !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Cho tam giác ABC , lấy điểm D trên cạnh AB, E trên cạnh AC. Hai đoạn BE, CD cắt nhau ở O, Nối D với E. Số tam giác tạo thành trong hình vẽ là 12 hình .
Đúng 0
Bình luận (0)
cho tam giác abc lấy d bên cạnh ab,e cạnh ac hai doan be cd cắt nhau ở o nối d với e tạo thành 12 hình
Đúng 0
Bình luận (0)
Tao thanh 12 hinh .
Minh chi noi ket qua thoi nhe
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
vẽ hình theo cách diển đạt sau (vẽ trên cùng một hình)
-vẽ 3 điểm D,E,G ko thẳng hàng
-vẽ tia DG , đường thẳng EG và đoạn thẳng DE
-vẽ tia Dy là tia đối của tia DE
-vẽ tia Da cắt đường thẳng EG tại M sao cho M nằm giữa E và G
Cho hình vuông ABCD,MN song song với hai cạnh AD và BC.Trên MN lấy điểm I,từ I vẽ đường thẳng song song với hai cạnh AD với BC,cắt AB tại E và CD tại F.Nối E với M và N.Ghi tên các hình chữ nhật,hình tam giác có trong hình vẽ