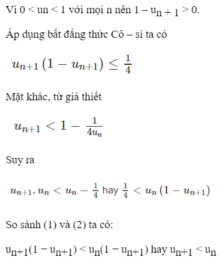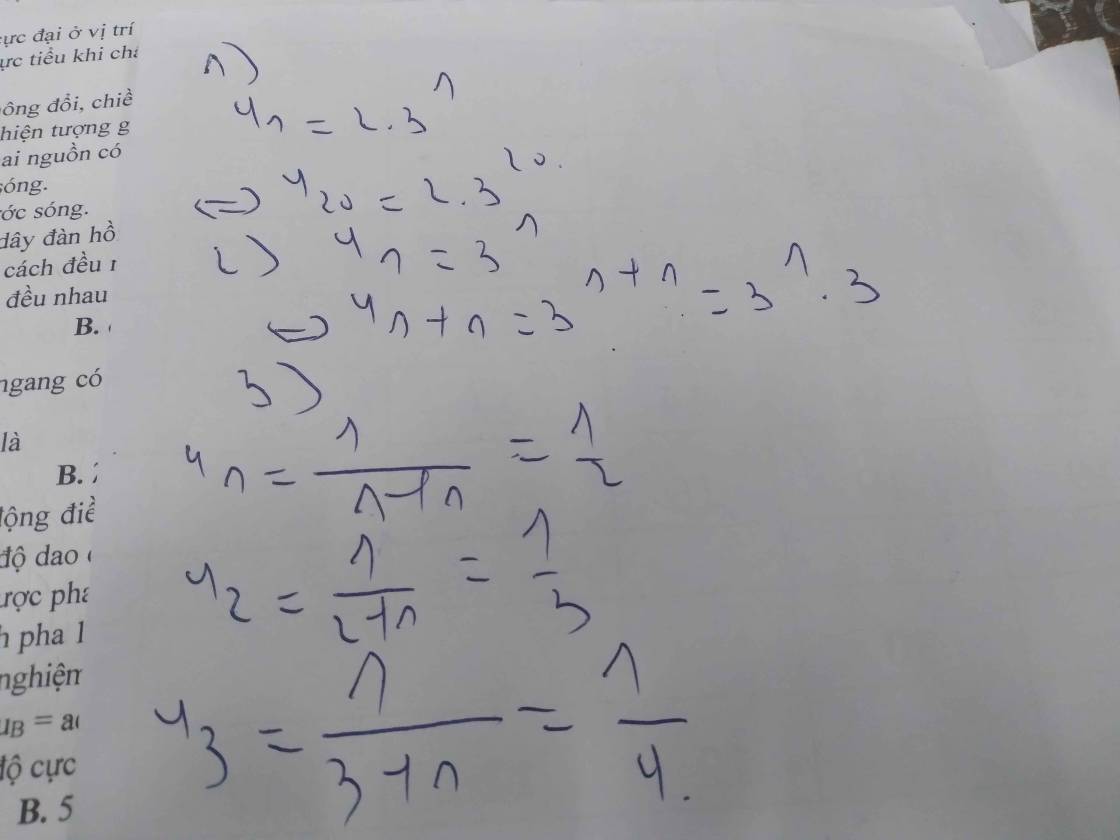Cho dãy : n+1;2n+3;3n+5;...
A_Viết số 100 trong dãy
B_tìm n sao cho tổng 100 số hạng đầu tiên bằng 60500

Những câu hỏi liên quan
Viết chương trình giải các bài toán sau :
(Mỗi bài 1 chương trình)
1) Cho 1 dãy gồm N phần tử .Tính tổng các phần tử CHẴN trong dãy.
2) Cho 1 dãy gồm N phần tử .Tìm giá trị LỚN nhất trong dãy (N \(\le\) 400).
3) Cho 1 dãy gồm N phần tử .Sắp xếp dãy theo chiều TĂNG dần.
CÁC BẠN GIÚP MÌNH VỚI ! CẢM ƠN !
Bài 1. Cho dãy số nguyên N và dãy a1, a2, a3, .., an (0N10^6; i0,1,2,…,N – 1; |a(i)|10^6.Yêu cầu: Cho N và dãy a1, a2, a3, …, an; xóa phần tử x và xuất mảng sau khi xóa.Bài 2. Cho dãy số nguyên N và dãy a1, a2, a3, …, an(0N10^6; i0,1,2,…,N – 1; |a(i)|10^6.Yêu cầu: Cho N và dãy a1, a2, a3, …, an; xóa các phần tử trùng nhau chỉ giữ lại một phần tử và xuất mảng sau khi xóa. Ai đó giúp mình 2 bài này theo pascal với được ko? Mình thật sự không biết làm :(( Ai đó giúp mình 2 bài này theo pascal với đ...
Đọc tiếp
Bài 1. Cho dãy số nguyên N và dãy a1, a2, a3, .., an (0<=N<=10^6; i=0,1,2,…,N – 1; |a(i)|<=10^6.Yêu cầu: Cho N và dãy a1, a2, a3, …, an; xóa phần tử x và xuất mảng sau khi xóa.
Bài 2. Cho dãy số nguyên N và dãy a1, a2, a3, …, an(0<=N<=10^6; i=0,1,2,…,N – 1; |a(i)|<=10^6.Yêu cầu: Cho N và dãy a1, a2, a3, …, an; xóa các phần tử trùng nhau chỉ giữ lại một phần tử và xuất mảng sau khi xóa.
Ai đó giúp mình 2 bài này theo pascal với được ko? Mình thật sự không biết làm :(( Ai đó giúp mình 2 bài này theo pascal với được ko? Mình xin cảm ơn nhiều!!
Bài 1:
uses crt;
var a:array[1..1000000]of longint;
i,n,x:longint;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
write('Nhap x='); readln(x);
for i:=1 to n do
if a[i]<>x then write(a[i]:4);
readln;
end.
Đúng 1
Bình luận (2)
Cho dãy số
(
u
n
)
thoả mãn điều kiện: Với mọi
n
∈
N
∗
thì
0
u
n
1
v
à
u
n
+
1
1
-
1...
Đọc tiếp
Cho dãy số ( u n ) thoả mãn điều kiện: Với mọi n ∈ N ∗ thì 0 < u n < 1 v à u n + 1 < 1 - 1 4 u n Chứng minh dãy số đã cho là dãy giảm.
1, Cho dãy A gồm N số nguyên a1,a2...aN. Hãy cho biết trong dãy có bao nhiêu số chẵn?
2, Cho N và dãy a1,a2...aN là dãy các số nguyên. Hãy cho biết trong dãy có bao nhiêu số âm
Câu 1: Cho dãy A là dãy giảm gồm N (N
Câu 1: Cho dãy A là dãy giảm gồm N (N<=250) số
nguyên dương A1....AN và số nguyên K. Hãy tìm kiếm số
nguyên K trong dãy A.
A. Xác định bài toán
- B. Viết thuật toán tìm kiếm nhị phân|cho bài
toán. viết 2 cách
Đúng 0
Bình luận (0)
#include <bits/stdc++.h>
using namespace std;
long long i,n,x,k;
int main()
{
cin>>n>>k;
for (i=1; i<=n; i++)
{
cin>>x;
if (x==k) cout<<i<<" ";
}
return 0;
}
Đúng 0
Bình luận (0)
1) cho dãy left(u_nright) xác đinh bởi u_n2.3^n giá trị của u_{20} với mọi số nguyên dương n là2) cho dãy số left(u_nright) biết u_n3^n số hạng u_{n+1} bằng3) cho dãy số left(u_nright), nin N* biết u_ndfrac{1}{n+1} ba số hạng đầu tiên của dãy số là
Đọc tiếp
1) cho dãy \(\left(u_n\right)\) xác đinh bởi \(u_n=2.3^n\) giá trị của \(u_{20}\) với mọi số nguyên dương n là
2) cho dãy số \(\left(u_n\right)\) biết \(u_n=3^n\) số hạng \(u_{n+1}\) bằng
3) cho dãy số \(\left(u_n\right)\), \(n\in N\)* biết \(u_n=\dfrac{1}{n+1}\) ba số hạng đầu tiên của dãy số là
Cho dãy số u1=-2;un+1=un+n-1(n€N) Số hạng thứ 5 của dãy số là
Ta có u2=u1+1=5?2=?1+1=5; u3=u2+2=7?3=?2+2=7; u4=u3+3=10?4=
?3+3=10. Do đó số hạng thứ 55 của dãy số là u5=u4+4=14?5=?4+4=14.
Vậy đáp án đúng 14
Đúng 0
Bình luận (0)
Xác định Input, output và viết thuật toán cho bài toán: Cho N và dãy số a1,a1,...,aN. Dãy số được gọi là đối xứng nếu ai = aN-i+1 với i = 1,...,N-1
Kiểm tra xem dãy đã cho có là dãy đối xứng hay không
input: Dãy số nguyên
Output: Kiểm tra xem dãy có đối xứng không
*Thuật toán
Bước 1: Nhập n và nhập dãy số
Bước 2: i←1; kt←true;
Bước 3: Nếu a[i]<>a[n-i+1] thì kt←false;
Bước 4: i←i+1;
Bước 5: Nếu i<=n thì quay lại bước 3
Bước 6: Nếu kt=true thì đây là dãy đối xứng và ngược lại
Bước 7: Kết thúc
Đúng 1
Bình luận (0)
Cho các dãy số :
u
n
n
2
+
1
,
v
n
n
+
1
n
,
x
n
2
n
+
1
,
y
n
n...
Đọc tiếp
Cho các dãy số :
u n = n 2 + 1 , v n = n + 1 n , x n = 2 n + 1 , y n = n n + 1 v ớ i m ọ i n ≥ 1
Trong các dãy số trên có bao nhiêu dãy bị chặn trên?
A. 1
B. 2
C. 3
D. 4
Chọn A
Trong bốn dãy số chỉ có yn=n/(n+1) < 1 nên có 1 dãy bị chặn trên
Đúng 0
Bình luận (0)
Cho dãy un xác định bởi \(u_1=1\)và \(\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\).Chứng minh dãy đó có giới hạn và tìm giới hạn dãy đó
Dễ thấy \(u_n>0,\forall n\inℕ^∗\).
Ta có \(u_{n+1}-u_n=\dfrac{u_n^2+2021}{2u_n}-u_n=\dfrac{2021-u_n^2}{2u_n}\)
Với \(n\ge2\) thì \(u_n=\dfrac{u_{n-1}^2+2021}{2u_{n-1}}\) \(=\dfrac{u_{n-1}}{2}+\dfrac{2021}{2u_{n-1}}\) \(>2\sqrt{\dfrac{u_{n-1}}{2}.\dfrac{2021}{2u_{n-1}}}\) \(=\sqrt{2021}\)
Vậy \(u_n>\sqrt{2021},\forall n\ge2\), suy ra \(u_{n+1}-u_n=\dfrac{2021-u_n^2}{2u_n}< 0,\forall n\inℕ^∗\)
\(\Rightarrow\) Dãy \(\left(u_n\right)\) là dãy giảm. Mà \(u_n>\sqrt{2021}\) \(\Rightarrow\left(u_n\right)\) có giới hạn hữu hạn. Đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L\) \(\Rightarrow L=\dfrac{L^2+2021}{2L}\) \(\Leftrightarrow L=\sqrt{2021}\)
Vậy \(\lim\limits_{n\rightarrow+\infty}u_n=\sqrt{2021}\)
Đúng 0
Bình luận (0)
Dễ thấy .
Ta có
Với thì
Vậy , suy ra
Dãy là dãy giảm. Mà có giới hạn hữu hạn. Đặt
Vậy
Đúng 0
Bình luận (0)
Xem thêm câu trả lời