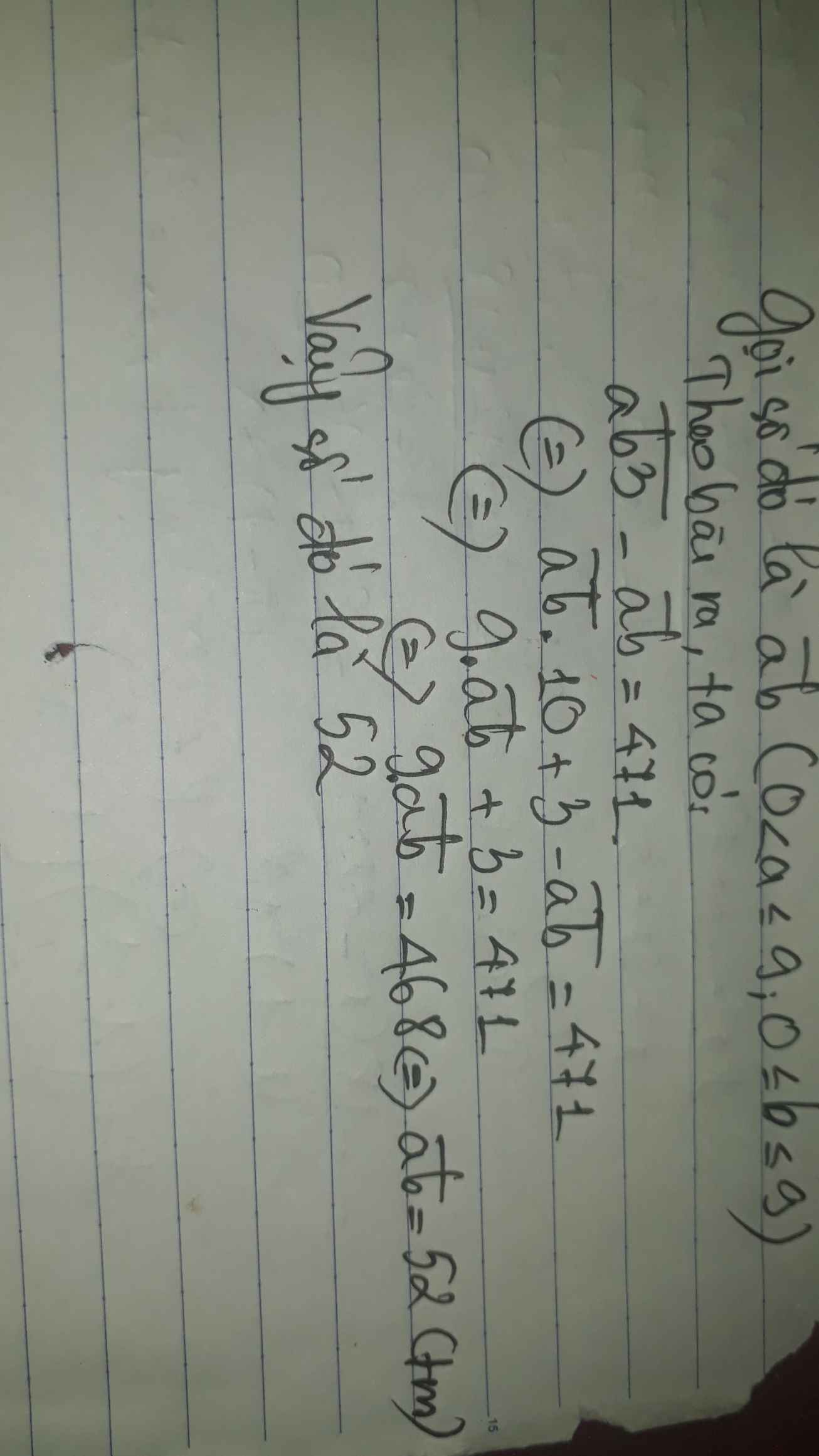Tìm số có hai chữ số. Biết rằng nếu thêm số 3 vào bên phải số đó thì được số mới. Tìm số mới. Biết rằng số mới hơn số đã cho 102 đơn vị.

Những câu hỏi liên quan
tìm số có 2 chữ số , biết rằng nếu viết thêm chữ số 3 vào bên phải số đó thì được số mới . tìm số đó biết rằng số mới đã cho 102 đơn vị.
Cho một số có hai chữ số. Biết rằng nếu viết thêm vào bên phải số đó hai chữ số thì được số mới lớn hơn số đã cho 1995 đơn vị. Tìm số có hai chữ số đó và phần viết thêm.
Số có hai chữ số có dạng: \(\overline{ab}\)
Khi viết thêm vào bên phải số đó hai chữ số: c;d
Thì được số mới có dạng: \(\overline{abcd}\)
Theo bài ra ta có: \(\overline{abcd}\) - \(\overline{ab}\) = 1995
\(\overline{ab}\) \(\times\) 100 + \(\overline{cd}\) - \(\overline{ab}\) = 1995
\(\overline{ab}\) \(\times\) ( 100 - 1) + \(\overline{cd}\) = 1995
\(\overline{ab}\) \(\times\) 99 + \(\overline{cd}\) = 1995
\(\overline{ab}\) \(\times\) 99 = 1995 - \(\overline{cd}\)
\(\overline{ab}\) = \(\dfrac{1995-\overline{cd}}{99}\)
\(\overline{ab}\) = 20 - \(\dfrac{cd-15}{99}\)
⇒ \(\overline{cd}\) - 15 ⋮ 99 vì \(\overline{cd}\) ≤ 99 ⇒ \(\overline{cd}\) = 15;
\(\overline{ab}\) = 20
Vậy số có hai chữ số ban đầu là 20; hai chữ số viết thêm là: 15
Đúng 3
Bình luận (0)
Tìm số có hai chữ số , biết rằng nếu viết thêm chữ số 3 vào tận cùng bên phải số đó thì được số mới hơn số phải tìm 192 đơn vị
Gọi số cần tìm là ab
Theo đề , ta có
ab3 = ab + 192
ab x 10 + 3 = ab + 192
ab x10 - ab = 192 - 3
ab x 9 = 189
ab = 189 : 9
ab = 21
tìm số tự nhiên có tận cùng là 3 biết rằng nếu thêm chữ số 2 vào bên phải số đó thì được số mới lớn hơn số đã cho 4079 đơn vị
Gọi số cần tìm là \(\overline{ab3}\)
Ta có :
\(\overline{ab32}-\overline{ab3}=4079\\ \overline{ab3}\cdot10+2-\overline{ab3}=4079\\ \overline{ab3}\cdot\left(10-1\right)=4079-2\\ \overline{ab3}\cdot9=4077\\ \overline{ab3}=4077:9\\ \overline{ab3}=453\)
Vậy số cần tìm là 453
Đúng 3
Bình luận (0)
tìm số có hai chữ số, biết rằng nếu viết thêm chữ số 3 vào tận cùng bên phải số đó thì được số mới hơn số phải tìm 192 đơn vị
Gọi số cần tìm là ab
Ta có : ab3 - ab = 192
ab x 10 + 3 - ab = 192
ab x 10 - ab = 192 - 3
ab x (10 - 1) = 189
ab x 9 = 189 => ab = 189 : 9 = 21
Đúng 1
Bình luận (0)
tìm số có hai chữ số,biết rằng nếu viết thêm chữ số 3 vào tận cùng bên phải số đó thì được số mới lớn hơn số phải tìm 192 đơn vị
Gọi số cần tìm là ab
Ta có: ab3 - ab = 192
ab x 10 + 3 - ab = 192
9 x ab + 3 = 192
9 x ab = 189
ab = 21
Vậy số cần tìm là 21
Đúng 0
Bình luận (0)
Gọi số cần tìm là ab
Theo đề , ta có
ab3 = ab + 192
ab x 10 + 3 = ab + 192
ab x 10 - ab = 192 - 3
ab x 9 = 189
ab = 189 : 9
ab = 21
Gọi số cần tìm là ab
Ta có: ab3 - ab = 192
ab x 10 + 3 - ab = 192
9 x ab + 3 = 192
9 x ab = 189
ab = 21
Vậy số cần tìm là 21
Xem thêm câu trả lời
tìm số tự nhiên có hai chữ số biết rằng khi viết thêm chữ số 2 vào bên phải số đó thì được số mới hơn số đã cho 405 đơn vị
Lời giải:
Gọi số cần tìm là $\overline{ab}$. Ta có:
$\overline{ab2}=405+\overline{ab}$
$\overline{ab}\times 10+2=405+\overline{ab}$
$\overline{ab}\times 10-\overline{ab}=405-2$
$\overline{ab}\times 9=403$
$\overline{ab}=403:9$ không phải số tự nhiên.
Đề có vẻ sai. Bạn xem lại.
Đúng 0
Bình luận (0)
Tìm số có hai chữ số biết rằng nếu viết thêm 0 vào bên phải số đó thì được số mới hơn số phải tìm 222 đơn vị
Theo bài ra, số cần tìm có dạng ab
Ta có :
ab + 222 = ab0
ab + 222 = 10 x ab
222 = ab x 9
ab = 222 : 9
ab = 74/3
=> Không thỏa mãn yêu cầu đề bài là số có hai chữ số
=> Bạn đã viết đề bài sai :))
Hok tốt !
#Minh#
Đúng 0
Bình luận (0)
Tìm số tự nhiên có hai chữ số biết rằng nếu viết thêm chữ số 3 vào bên phải số đó thì ta được số mới hơn số cũ 471 đơn vị
Lời giải:
Gọi số cần tìm là $\overline{ab}$. Điều kiện: $a,b$ là số tự nhiên; $a,b\leq 9; a\neq 0$
Theo bài ra ta có:
$\overline{ab3}-\overline{ab}=471$
$\overline{ab}\times 10+3-\overline{ab}=471$
$\overline{ab}\times (10-1)+3=471$
$\overline{ab}\times 9+3=471$
$\overline{ab}\times 9=468$
$\overline{ab}=468:9=52$
Vậy số cần tìm là $52$
Đúng 1
Bình luận (0)
Giải:
Gọi số cần tìm là x, ta có:
x3 - x = 471
x. 10 + 3 - x = 471
10x - x + 3 = 471
9x + 3 =471
9x = 471 - 3
9x = 468
x = 468 : 9
x = 52
Vậy số cần tìm là 52.
*Dấu chấm trên bài là dấu nhân nha*
Đúng 0
Bình luận (0)
Xem thêm câu trả lời