Cho tứ diện ABCD (H.2.13). Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \).
Những câu hỏi liên quan
Cho hình tứ diện ABCD. Gọi M. N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng :
a) \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}=2\overrightarrow{MN}\)
b) \(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}=2\overrightarrow{PQ}\)
Chứng minh rằng đối với tứ giác ABCD bất kì ta luôn có :
a) \(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{O}\)
b) \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CB}-\overrightarrow{CD}\)
Cho tứ giác ABCD. Gọi E, F, O lần lượt là trung điểm của AC, BD, EF. Chứng minh:
\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}\)
\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{BD}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{CB}=\overrightarrow{AD}+\overrightarrow{CB}\)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OE}+\overrightarrow{EA}\right)+\left(\overrightarrow{OF}+\overrightarrow{FB}\right)+\left(\overrightarrow{OE}+\overrightarrow{EC}\right)+\left(\overrightarrow{OF}+\overrightarrow{FD}\right)\)
\(=2\left(\overrightarrow{OE}+\overrightarrow{EF}\right)+\left(\overrightarrow{EA}+\overrightarrow{EC}\right)+\left(\overrightarrow{FB}+\overrightarrow{FD}\right)\)
\(=2.\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\)
Đúng 0
Bình luận (0)
Cho hình tứ diện ABCD. Chứng minh rằng :
a) \(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}\)
b) \(\overrightarrow{AB}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{CD}+\overrightarrow{DB}\)
Cho tứ giác ABCD và M , N lần lượt là trung điểm của đoạn thẳng AB , CD . Chứng minh rằng :
a / overrightarrow{CA}+overrightarrow{DB}overrightarrow{CB}+overrightarrow{DA}2overrightarrow{MN}
b / overrightarrow{AD}+overrightarrow{BD}+overrightarrow{AC}+overrightarrow{BC}4overrightarrow{MN}
c / Gọi I là trung điểm của BC . Chứng minh rằng : 2left(overrightarrow{AB}+overrightarrow{AI}+overrightarrow{NA}+overrightarrow{DA}right)3overrightarrow{DB}
HELP ME !!!!!!!!!!!
Đọc tiếp
Cho tứ giác ABCD và M , N lần lượt là trung điểm của đoạn thẳng AB , CD . Chứng minh rằng :
a / \(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{DA}=2\overrightarrow{MN}\)
b / \(\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{BC}=4\overrightarrow{MN}\)
c / Gọi I là trung điểm của BC . Chứng minh rằng : \(2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{NA}+\overrightarrow{DA}\right)=3\overrightarrow{DB}\)
HELP ME !!!!!!!!!!!
a) Chữa đề: \(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{DA}=2\overrightarrow{NM}\)
\(Ta\text{ }có:\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AB}\\ =\overrightarrow{CB}+\overrightarrow{DA}+\left(\overrightarrow{BA}+\overrightarrow{AB}\right)=\overrightarrow{CB}+\overrightarrow{DA}\)
\(\)\(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CA}+\overrightarrow{CB}+\overrightarrow{DC}\\ =2\overrightarrow{CM}+2\overrightarrow{NC}=2\left(\overrightarrow{NC}+\overrightarrow{CM}\right)=2\overrightarrow{NM}\)
Vậy \(\overrightarrow{CA}+\overrightarrow{DB}=\overrightarrow{CB}+\overrightarrow{DA}=2\overrightarrow{NM}\)
\(\text{b) }\overrightarrow{AD}+\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{BC}=-\left(\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{CA}+\overrightarrow{CB}\right)\\ =-\left[\left(\overrightarrow{DA}+\overrightarrow{DB}\right)+\left(\overrightarrow{CA}+\overrightarrow{CB}\right)\right]\\ =-\left(2\overrightarrow{DM}+2\overrightarrow{CM}\right)=2\left(\overrightarrow{MD}+\overrightarrow{MC}\right)=4\left(\overrightarrow{MN}\right)\)
\(\text{c) }2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{NA}+\overrightarrow{DA}\right)\\ =2\left[\left(\overrightarrow{AB}+\overrightarrow{DA}\right)+\left(\overrightarrow{AI}+\overrightarrow{NA}\right)\right]\\ =2\left[\left(\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{DB}\right)+\overrightarrow{NI}\right]=2\left(\overrightarrow{DB}+\overrightarrow{NI}\right)\)
Mà IN là dường trung bình \(\Delta BCD\)
\(\Rightarrow\left\{{}\begin{matrix}IN//BD\\IN=\frac{1}{2}BD\end{matrix}\right.\Rightarrow\overrightarrow{IN}=\frac{1}{2}\overrightarrow{BD}\\ \Rightarrow2\left(\overrightarrow{AB}+\overrightarrow{AI}+\overrightarrow{NA}+\overrightarrow{DA}\right)\\ =2\left(\overrightarrow{DB}+\overrightarrow{NI}\right)=2\left(\overrightarrow{DB}+\frac{1}{2}\overrightarrow{DB}\right)=2\cdot\frac{3}{2}\overrightarrow{DB}=3\overrightarrow{DB}\)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD
a) Chứng minh rằng \(\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0\)
b) Từ đẳng thức trên hãy suy ra rằng nếu tứ diện ABCD có \(AB\perp CD\) và \(AC\perp DB\) thì \(AD\perp BC\)
Cho hình thang ABCD có đáy là AB và CD. Cho biết \(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} ;\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} \). Chứng minh rằng hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
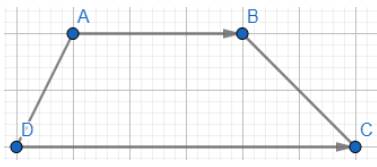
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
Đúng 0
Bình luận (0)
cho ABCD là hình thang có đáy AB , CD sao cho AB = 2CD . Từ C vẽ \(\overrightarrow{CI}=\overrightarrow{DA}\) . Chứng minh rằng
a, \(\overrightarrow{AD}=\overrightarrow{IC}\)
b, \(\overrightarrow{AI}=\overrightarrow{IB}\)\(=\overrightarrow{DC}\)
C , \(\overrightarrow{DI}=\overrightarrow{CB}\)
CHo hình bình hành ABCD có O là giao điểm của 2 đường chéo. Chứng minh:
a, overrightarrow{AC}-overrightarrow{BA}overrightarrow{AD}; | overrightarrow{AB}+overrightarrow{AD}| overrightarrow{AC}
b, NẾu |overrightarrow{AB}+overrightarrow{AD}||overrightarrow{CB}-overrightarrow{CD|} thì ABCD là hình chữ nhật
Đọc tiếp
CHo hình bình hành ABCD có O là giao điểm của 2 đường chéo. Chứng minh:
a, \(\overrightarrow{AC}-\overrightarrow{BA}=\overrightarrow{AD};\) \(|\) \(\overrightarrow{AB}+\overrightarrow{AD}\)\(|\) \(=\overrightarrow{AC}\)
b, NẾu \(|\overrightarrow{AB}+\overrightarrow{AD}|=|\overrightarrow{CB}-\overrightarrow{CD|}\) thì ABCD là hình chữ nhật
Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)
Ta có:
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} \)
Mặt khác: \(\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \)
\(\begin{array}{l} \Rightarrow 2\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} + \overrightarrow {MB} + \overrightarrow {BC} + \overrightarrow {CN} \\ \Leftrightarrow 2\overrightarrow {MN} = \left( {\overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {DN} + \overrightarrow {CN} } \right) + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow {BC} + \overrightarrow {AD} \\ \Leftrightarrow 2\overrightarrow {MN} = \overrightarrow {BC} + \overrightarrow {AD} \end{array}\)
Lại có:
\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BD} + \overrightarrow {DC} + \overrightarrow {AD} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {BD} = \overrightarrow {AC} + \overrightarrow {BD} .\)
Vậy \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)
Đúng 0
Bình luận (0)