Cho tam giác ABC đều M bất kì trong tam giác ABC.Từ M kẻ các đường vuông góc đến các cạnh AB,BC,AC lần lượt cắt các cạnh đấy tại N,P,Q a)C/m MN+MP+MQ không đổi khi m thay đổi
b) 3 cạnh MN ,MP,MQ là 3 cạnh của tam giác
Những câu hỏi liên quan
Cho tam giác ABC đều M bất kì trong tam giác ABC.Từ M kẻ các đường vuông góc đến các cạnh AB,BC,AC lần lượt cắt các cạnh đấy tại N,P,Q a C m MN MP MQ không đổi khi m thay đổib 3 cạnh MN ,MP,MQ là 3 cạnh của tam giác
Cho tam giác ABC đều, các đường cao AD, BH, CK của tam giác cắt nhau tại O. M là một điểm bất kì trên cạnh BC (M không trung với B, C, D) .Kẻ MP và MQ lần lượt vuông góc với AB và AC. PQ cắt OM tại R. Chứng minh rằng R la trung điểm PQ
Cho tam giác cân ABC. Từ điểm M trên cạnh đáy BC vẽ các đường MP, MQ lần lượt vuông góc với AB, AC. CM: MP+MQ không phụ thuộc vào vị trí của M trên cạnh BC
Ta co \(MP=MB.\sin\widehat{B},MQ=MC.\sin\widehat{C}\)
=> \(MP+MQ=\left(MB+MC\right).\sin\widehat{B}=BC.\sin\widehat{B}=const\)
Cho tam giác ABC có đường cao AH .Trên cạnh BC lấy điểm M bất kì ( M không trùng với B ,C ,H ) từ M kẻ MP và MQ vuông góc với các cạnh AB ,AC
1.Chứng minh APMQ là tứ giác nội tiếp và hãy xác định tâm O của đường tròn ngoại tiếp tứ giác đó .
2.Chứng minh rằng MP+MQ=AH .
3.Chứng minh OH vuông góc với PQ.
Cho tam giác ABC đểu đường cao AH. Trên cạnh BC lấy điểm M bất kì (M không trùng B,C,H). Từ M kẻ MP, MQ lần lượt vuông gióc với AB,AC(P thuộc AB,Q thuộc AC)
1, Chứng minh APMQ nội tiếp
2, Gọi O là tâm đường tròn ngoại tiếp tứ giác APMQ. Chứng minh OH vuông góc với PQ
3, Chứng minh MP+MQ=AH
1 Cho tam giác ABC cân tại A đường cao AH. M là một điểm bất kì trên cạnh BC. Kẻ đường thẳng qua M và song song với AH cắt AB và AC lần lượt tại N và Qa, CM tam giác ANQ cân b, Tính các góc của tam giác ANQ biết góc ABC70c,Kẻ AI vuông góc với MQ. CM AI song song với BC và AIMH2 Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M trên tia đối của tia CA lấy N sao cho AM+AN2AB. CMR:a, BMCNb,BC cắt MN tại trung điểm I của MN
Đọc tiếp
1 Cho tam giác ABC cân tại A đường cao AH. M là một điểm bất kì trên cạnh BC. Kẻ đường thẳng qua M và song song với AH cắt AB và AC lần lượt tại N và Q
a, CM tam giác ANQ cân
b, Tính các góc của tam giác ANQ biết góc ABC=70
c,Kẻ AI vuông góc với MQ. CM AI song song với BC và AI=MH
2 Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M trên tia đối của tia CA lấy N sao cho AM+AN=2AB. CMR:
a, BM=CN
b,BC cắt MN tại trung điểm I của MN
Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của BC. Trên cạnh AB và AC lấy các điểm P, Q sao cho MP, MQ lần lượt vuông góc với AB, AC.
Xem chi tiết
a, Chứng minh rằng MP = MQ và AP = AQ.
b, Đường thẳng PQ có vuông góc với AM không? Vì sao?
VẼ HÌNH GIÚP MÌNH NHA. CẢM ƠN Ạ
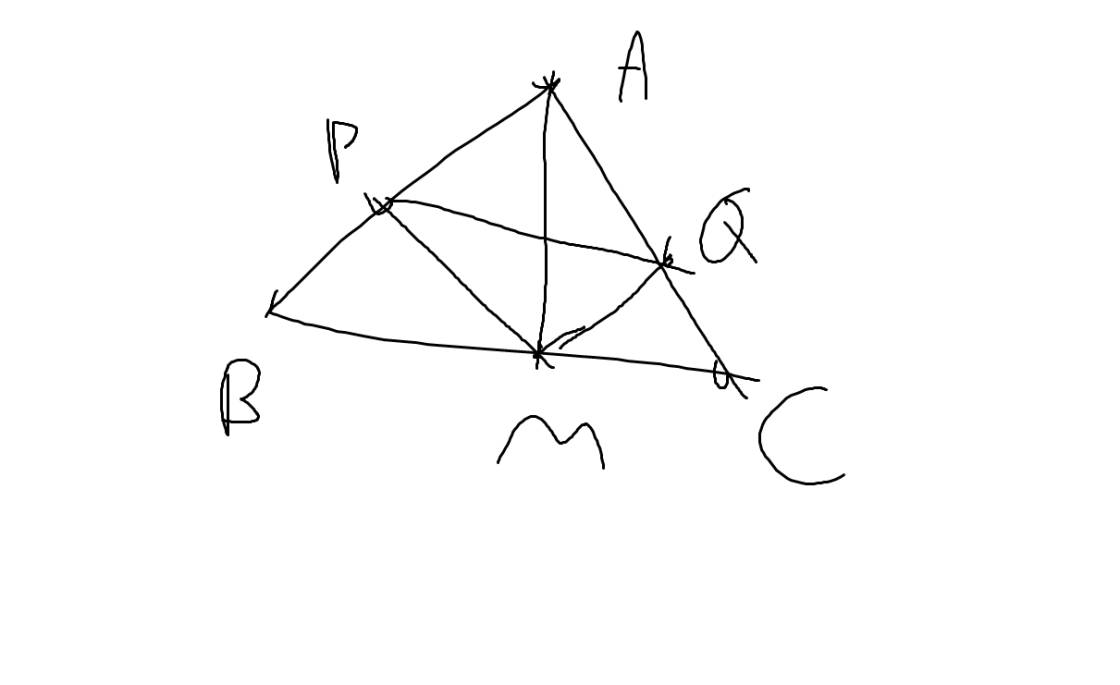
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ
Đúng 2
Bình luận (0)
Cho tam giác đều ABC. Đường cao AH.M là một điểm thuộc cạnh BC(M khác A và B).từ M kẻ MP,MQ lần lượt vuông góc với AB,AC.
a/Chứng minh MP+MQ không đổi
b/Gọi O là trung điểm của AM.tứ giác POQH là hình gì
c/tìm vị trí của M trên BC để độ dài PQ là ngắn nhất
Cho tam giác ABC đều ,có đường cao AH (H thuộc BC ).Trên cạnh BC lấy điểm M bất kỳ ( M không trùng với B,C,H ) ; gọi P,Q lần lượt là hình chiếu vuông góc của M lên các cạnh AB,AC .
a) CM tứ giác APMQ nội tiếp một đường tròn
b) chứng minh MP +MQ = AH
c) gọi O là tâm đường tròn ngoại tiếp tứ giác APMQ . chứng minh OH vuông góc với PQ ?
A) MP vuông góc AB tại P => góc MPA=90; MQ vuông góc AC tại Q=> MQA=90
=> tg APMQ nội tiếp(tổng 2 góc đối =90)
b) diện tích tam giác AMB=1/2.MP.AB=1/2.MP.BC; diện tích tam giác AMC=1/2.MQ.AC=1/2.MP.BC( AB=BC=CA tam giác đều)
S tam giác ABC=1/2.AH.BC
ta có: S AMB+S AMC=S ABC <=> \(\frac{1}{2}.MP.BC+\frac{1}{2}MQ.BC=\frac{1}{2}AH.BC\Leftrightarrow\frac{1}{2}BC\left(MP+MQ\right)=\frac{1}{2}.BC.AH\)
=> MP+MQ=AH
c) góc AHM=90(AH là đường cao)=> H cũng thuộc đường tròn đường kính AM <=> ngũ giác APMQH nội tiếp
(O): góc HAQ=1/2 góc HOQ(góc nt và góc ở tâm)
tam giác AHC vuông => góc HAC=90-C=90-60=30 độ hay HAQ=30(góc C=60 vì tam giác đều)
=> góc HOQ=2.30=60 .
(O): góc PAQ=1/2 góc POQ(góc nt và góc ở tâm) <=> góc POQ=2.60=120( góc PAQ hay BAC=60- tam giác đều)
góc HOQ=60 => OH là pg của góc POQ.
tam giác POQ có: OP=OQ=R=> tam giác cân => OH đồng thời là đường cao => OH vuông góc PQ
Đúng 1
Bình luận (0)
câu a , tổng hai góc đối là 180 độ nhé bạn