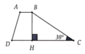
Cho hình thang cân ABCD(AB//CD), CD là đáy lớn. Gọi AH là đường cao (H∈CD) vàHC=5cm. Độ dài đường trung bình của hình thang là ?(cm)
Gợi ý : Kẻ BK⊥CD tại K, tính tổng AB+CD theo HC.
Cho hình thang ABCD( AB // CD). DC là đáy lớn, AH là đường cao. DH= 5cm, HN = 35cm. Tính độ dài đường trung bình của hình thang đó.
Cho hình thang cân ABCD (AB // CD) AB < CD có đường cao AH. Gọi M, N lần lượt là trung điểm của AD và BC. Tính độ dài đoạn MN biết HC = 5cm.
Tam giác AHD vuông tại H có HM là đường trung tuyến ứng với cạnh huyền AD
\(\Rightarrow HM=MD=\frac{1}{2}AD\)
\(\Rightarrow\Delta HMD\)cân tại M \(\Rightarrow\widehat{D}=\widehat{MHD}\)
Mà \(\widehat{D}=\widehat{C}\left(gt\right)\Rightarrow\widehat{MHD}=\widehat{C}\Rightarrow MH//NC\)
Mặt khác, \(HM=\frac{1}{2}AD=\frac{1}{2}BC=NC\)
Tứ giác MNHC có: MH // NC và MH = NC
Do đó: MHCN là hình bình hành (DHNB) \(\Rightarrow MN=HC=5cm\)
Cho hình thang cân ABCD có AB // CD và AB < CD. Kẻ đường cao AH, BK của hình thang ABCD (H, K thuộc CD).
1) Chứng minh tam giác ADH bằng tam giác BCK.
2) Gọi O là giao điểm của AC và BD; I là giao điểm của AD và BC. Chứng minh OI là trung trực của AB.
3) Giả sử BK=AB+CD/2. Tính góc tạo bởi hai đường chéo của hình thang.
cho hình thang abcd (ab//cd) có ah và bk là 2 đg cao của hình thang
a) cm DH=(cd-ab):2
b) bik AB= 6cm, CD=5cm, tính dh,ah và diện tích hình thang cân abcd
Bài 1:Cho hình thang cân ABCD ( AB// CD) có AB = 3 cm, CD = 6 cm, AD = 2,5 cm. Vẽ 2 đường cao AH, BK. Tính DH, DK, AH.
Bài 2: Cho hình thang ABCD (AB//CD) có AC = BD. Qua B kẻ đường thẳng song song vs AC, cắt đường thẳng DC tại E. Chứng minh rằng:
a) Tam giác BDE là tam giác cân.
b) Hình thang ABCD là hình thang cân.
Cho hình thang cân ABCD AB // CD đáy nhỏ AB =3cm đường cao AH=5 cm góc D=45 độ
Tính độ dài của đáy lớn CD
kẻ BK\(\perp\)DC
Xét ΔAHD vuông tại H có \(tanD=\dfrac{AH}{HD}\)
=>\(\dfrac{5}{HD}=tan45=1\)
=>HD=5/1=5(cm)
Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
\(\widehat{D}=\widehat{C}\)
Do đó: ΔAHD=ΔBKC
=>DH=KC
mà DH=5cm
nên KC=5cm
Ta có: AB//DC
\(H,K\in DC\)
Do đó: AB//HK
Ta có: AH\(\perp\)DC
BK\(\perp\)DC
Do đó: AH//BK
Xét tứ giác ABKH có
AB//KH
AH//BK
Do đó: ABKH là hình bình hành
=>AB=HK=3cm
DC=DH+HK+KC
=5+5+3
=13(cm)
Hình thang cân ABCD có đáy nhỏ AB = 14 cm , đáy lớn CD có độ dài gắp đôi đáy nhỏ , đường cao AH = nửa tổng hai đáy . Bình phương độ dài cạnh bên của hình thang đó là
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
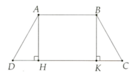
Cho hình thang cân ABCD (AB // CD) có AH và BK là hai đường cao của hình thang.
a) Chứng minh DH = C D − A B 2 .
b) Biết AB = 6 cm, CD = 14 cm, AD = 5 cm, tính DH, AH và diện tích hình thang cân ABCD.
a) Chứng minh
DADH = DBCK (ch-gnh)
Þ DH = CK
Vận dụng nhận xét hình thang ABKH (AB//KH) có AH//BK Þ AB = HK
b) Vậy D H = C D − A B 2
c) DH = 4cm, AH = 3cm; SABCD = 30cm2
Cho hình thang cân ABCD (AB//CD, AB < CD). Kẻ đường cao AH.
Biết AH = 8 cm, HC = 12 cm. Tính diện tích hình thang ABCD
Kẻ BK ^CD tại K Þ AB = HK
S A B C D = ( 2 H K ) + 2 K C ) . A H 2 = H C . A H = 96 c m 2