Ta đã biết nếu G' là trọng tâm tam giác ABC thì:
\(\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\).
Gỉa sử có điểm G thỏa mãn: \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
Ta sẽ chứng minh \(G\equiv G'\).
Thật vậy:
\(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}+\overrightarrow{G'A}+\overrightarrow{G'B}+\overrightarrow{G'C}=\overrightarrow{0}\)
\(\Leftrightarrow3\overrightarrow{GG'}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GG'}=\overrightarrow{0}\).
Vậy \(G\equiv G'\).

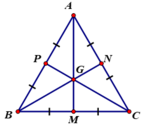
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.

Khi đó AM, BN, CP đồng quy tại trọng tâm G.

Ta có: ∆ABC đều suy ra:

+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).

+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).

⇒ AM = BN = CP (1)

Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:

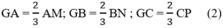
Từ (1) , (2) ⇒ GA = GB = GC.

Gọi `AM` là trung tuyến của `ΔABC`

`=>AM` đồng thời là đường cao 

`=>ΔAMB;ΔAMC⊥M`

`AM` là trung tuyến nên 

`BM=MC=(BC)/2=4(cm)`

Áp dụng định lý py-ta-go ta tính được 

`AM^2=AB^2-BM^2=5^2-4^2=25-16=9(cm)`

`=>AM=3cm`

`G` trọng tâm 

`=>GA=2/3AM=2cm`

`GM=1/3AM=1cm`

Áp dụng định lý py-ta-go lần nữa ta tính đc

`GC^2=BG^2=BM^2+GM^2=4^2+1^2=16+1=17cm`

`=>GB=GC=`\(\sqrt{17cm}\)

Đề có sai không bạn , nếu `Delta ABC` là tam giác thường thôi thì không cm đc đâu ạ 

mk bận đi ch nên chỉ tạm câu a nha 

vẽ 3 đường trung tuyến AD ; BE ; CF 

VT = 

\(GA+GB+GC\)   ( nhớ thêm dấu vec tơ nha ) 

\(=-\frac{2}{3}AD-\frac{2}{3}BE-\frac{2}{3}CF\)  

\(=-\frac{2}{3}\cdot\frac{1}{2}\left(AB+BC\right)-\frac{2}{3}\cdot\frac{1}{2}\left(BA+BC\right)-\frac{2}{3}\cdot\frac{1}{2}\left(CA+CB\right)\)     ( quy tắc hình bình hành ) 

\(=-\frac{1}{3}\left(AB+AC\right)-\frac{1}{3}\left(BA+BC\right)-\frac{1}{3}\left(CA+CB\right)\) 

\(=-\frac{1}{3}AB-\frac{1}{3}AC-\frac{1}{3}BA-\frac{1}{3}BC-\frac{1}{3}CA-\frac{1}{3}CB\)    

\(=0=VP\)

.... chua hoc