Cho tam giác ABC có góc ABC =35°; góc ACB =65° a, Tính số đo góc BAC b, Tìm cạnh lớn nhất và bé nhất của tam giác ABC c, Vẽ AI vuông góc với BC ( I thuộc cạnh BC ). Trên đoạn AI lấy điểm D, trên đoạn IB lấy điểm E. Chứng minh DE < AB

Những câu hỏi liên quan
Mình cần gấp ạ....
1)Cho tam giác ABC cân tại A có AB=6 cm,BC=4 cm.Tính các góc trong tam giác ABC.
2)Cho tam giác ABC vuông tại A có góc B=50 độ,BC=5 cm.Ở phía ngoài tam giác ABC,vẽ tam giác vuông ADC có góc CAD=35 độ.Tính chu vi tam giác ABC và chu vi tam giác ADC
Bài 1: Cho tam giác ABC vuông tại A giải Tam giác ABC biết: a) Góc B 35 độ, BC40 cmb) AB70cm, AC60cmc) AB6cm, góc B60 độd) AB5cm, AC7cm 2) Cho tam giác ABC góc A 90 độ đường cao AH biết HB25cm, HC 64cm tín số đo góc B và C3)Tam giác ABC có góc A 90 độ, AB21cm, ggos C 40 độ tính độ dài đường phân giác BD4) Tam giác ABC có góc B70 độ góc C35 độ đường cao AH5cm tính độ dài AB,AC,B
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A giải Tam giác ABC biết: a) Góc B= 35 độ, BC=40 cm
b) AB=70cm, AC=60cm
c) AB=6cm, góc B=60 độ
d) AB=5cm, AC=7cm
2) Cho tam giác ABC góc A =90 độ đường cao AH biết HB=25cm, HC =64cm tín số đo góc B và C
3)Tam giác ABC có góc A =90 độ, AB=21cm, ggos C =40 độ tính độ dài đường phân giác BD
4) Tam giác ABC có góc B=70 độ góc C=35 độ đường cao AH=5cm tính độ dài AB,AC,B
cho tam giác ABC có góc BAC 50 độ, góc ACB 70 độ. lấy điểm I nằm trong tam giác ABC sao cho góc IBC 30 độ, góc ICB 35 độ.a) tính số đo góc ABC; b) chứng minh rằng các tia BI, CI lần lượt là tia phân giác của góc ABC, ACB; c) gọi D, E, F lần lượt là hình chiếu vuông góc của điểm I trên các đường thẳng BC, CA, AB. Chứng minh rằng I là giao điểm của 3 đường trung trực của tam giác DEF
Đọc tiếp
cho tam giác ABC có góc BAC =50 độ, góc ACB =70 độ. lấy điểm I nằm trong tam giác ABC sao cho góc IBC =30 độ, góc ICB =35 độ.
a) tính số đo góc ABC; b) chứng minh rằng các tia BI, CI lần lượt là tia phân giác của góc ABC, ACB; c) gọi D, E, F lần lượt là hình chiếu vuông góc của điểm I trên các đường thẳng BC, CA, AB. Chứng minh rằng I là giao điểm của 3 đường trung trực của tam giác DEF
a: góc ABC=180-50-70=60 độ
b: Vì góc IBC=1/2*góc ABC
nên BI là phân giác của góc ABC
Vì góc ICB=1/2*góc ACB
nên CI là phân giác của góc ACB
c: Xét ΔBFI vuông tại F và ΔBDI vuông tại D có
BI chung
góc FBI=góc DBI
=>ΔBFI=ΔBDI
=>ID=IF
Xét ΔCDI vuông tại D và ΔCEI vuông tại E co
CI chung
góc DCI=góc ECI
=>ΔCDI=ΔCEI
=>ID=IE=IF
=>I là giao của 3 đường trung trực ΔDEF
Đúng 0
Bình luận (0)
1.Cho tam giác ABC có góc B=70 độ, góc C= 35 độ, đường cao AH = 5cm. Tính các cạnh của tam giác ABC.
tam giác abc cân tại a có góc bac = 100 M nằm trên ABC sao cho góc MBC=35 góc MCB 30 tính BAM
tam giác ABC có góc B bằng 60, góc C bằng 50 , AC bằng 35 cm tính diện tích tam giác ABC
trên hình kẻ đường cao AH
ta có \(\text{cos 50}=\frac{HC}{AC}\Rightarrow HC=AC.\text{cos 50 }=35.\text{cos 50}\approx22\text{ (cm)}\)
\(\text{sin 50}=\frac{AH}{AC}\Rightarrow AH=AC.\text{sin 50}=35.\text{sin 50}\approx27\left(cm\right)\)
\(\text{tan 60}=\frac{AH}{BH}\Rightarrow BH=\frac{AH}{\text{tan 60}}=\frac{27}{\text{tan 60}}\approx16\left(cm\right)\)
\(\Rightarrow BC=22+16=38\left(cm\right)\)
\(\text{sin 60}=\frac{AH}{AB}\Rightarrow AB=\frac{AH}{\text{sin 60}}=\frac{27}{\text{sin 60}}\approx31\left(cm\right)\)
Diện tích tam giác ABC là:
35+38+31=104 (cm)
Đúng 0
Bình luận (0)
tam giác ABC có góc B bằng 60, góc C bằng 50 , AC bằng 35 cm tính diện tích tam giác ABC
Cho tam giác ABC có góc A=90 độ,BC=5,góc B=35 độ .Hãy giải tam giác vuông đó.
Cho tam giác ABC vuông tại A,Giải tam giác ABC biết
a,AC=15cm góc C=35 độ
b,AB=8cm,góc C=50 độ
a: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=55^0\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)
=>\(BC=15:sin55\simeq18.31\left(cm\right)\)
\(AB=\sqrt{BC^2-AC^2}\simeq10,5\left(cm\right)\)
b: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=90^0-50^0=40^0\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)
=>\(BC=8:sin50\simeq10,44\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq6,71\left(cm\right)\)
Đúng 0
Bình luận (0)
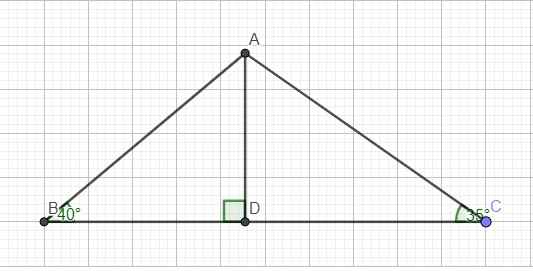
Cho tam giác ABC . Có góc B = 40 độ , góc C = 35 độ , BC = 20cm . tính AC
Kẻ đường cao AD ứng với BC
Trong tam giác vuông ABD:
\(cotB=\dfrac{BD}{AD}\Rightarrow BD=AD.cotB\)
Trong tam giác vuông ACD:
\(cotC=\dfrac{CD}{AD}\Rightarrow CD=AD.cotC\)
\(\Rightarrow BD+CD=AD.cotB+AD.cotC\)
\(\Rightarrow BC=AD\left(cotB+cotC\right)\)
\(\Rightarrow AD=\dfrac{BC}{cotB+cotC}\)
Trong tam giác vuông ACD:
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{BC}{sinC\left(cotB+cotC\right)}=\dfrac{20}{sin35^0\left(cot40^0+cot35^0\right)}=13,3\left(cm\right)\)
Đúng 2
Bình luận (0)