Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfrac{SA}{SA'}+\dfrac{SC}{SC'}-\left(\dfrac{SB}{SB'}+\dfrac{SD}{SD'}\right)\)

Những câu hỏi liên quan
Hình chóp S.ABCD có đáy là hình bình hành ABCD. Giả sử M thuộc đoạn thẳng SB. Mặt phẳng (ADM) cắt hình chóp S.ABCD theo thiết diện là hình:
A.tam giác
B. hình thang
C. hình bình hành
D.hình thoi
Do AD//BC, M thuộc (SBC) nên giao tuyến của (ADM) với (SBC) là đường thẳng qua M và song song với BC, đường thẳng này cắt SC tại N.
Ta có MN//AD. Vậy thiết diện là hình thang AMND.
Đáp án B
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I là trung điểm của SA, thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là A. Tam giác IBC. B. Hình thang IJCB (J là trung điểm SD ). C. Hình thang IGBC (G là trung điểm SB ). D. Tứ giác IBCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. I là trung điểm của SA, thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (IBC) là
A. Tam giác IBC.
B. Hình thang IJCB (J là trung điểm SD ).
C. Hình thang IGBC (G là trung điểm SB ).
D. Tứ giác IBCD
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết rằng SAperp mpleft(ABCDright) , gọi M là hình chiếu vuông góc của A lên cạnh SD . Giả sử rằng AB2.AD2.DC2.a , độ dài cạnh SA2a Tính khoảng cách từ điểm M đến mpleft(SBCright)P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em với ạEm cám ơn nhiều ạ!
Đọc tiếp
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\). Biết rằng \(SA\perp mp\left(ABCD\right)\) , gọi M là hình chiếu vuông góc của \(A\) lên cạnh \(SD\) .
Giả sử rằng \(AB=2.AD=2.DC=2.a\) , độ dài cạnh \(SA=2a\)
Tính khoảng cách từ điểm \(M\) đến \(mp\left(SBC\right)\)
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em với ạ
Em cám ơn nhiều ạ!
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành,
A
B
a
,
S
A
a
3
và
S
A
⊥
A
B
C
D...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, A B = a , S A = a 3 và S A ⊥ A B C D . Tính góc giữa hai đường thẳng SB và CD
A. 600.
B. 300.
C. 450.
D. 900.
Chọn đáp án A
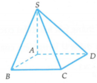
Ta có ABCD là hình bình hành nên CD//AB.
Lại có S A ⊥ A B C D ⇒ S A ⊥ A B
⇒ ∆ S A B vuông tại A.
Suy ra
![]()
Trong tam giác SAB vuông tại A có
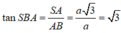
⇒ S B A ⏜ = 60 0
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có SA
⊥
(ABCD), đáy ABCD là hình bình hành có AB
⊥
AC. Biết SA AD a. Tính khoảng cách h từ A tới mặt phẳng (SCD). A. h
a
2
2
B. h
a
3
7
C. h
a
3
2
D. h
a
2
Đọc tiếp
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hình bình hành có AB ⊥ AC. Biết SA = AD = a. Tính khoảng cách h từ A tới mặt phẳng (SCD).
A. h = a 2 2
B. h = a 3 7
C. h = a 3 2
D. h = a 2
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua trung điểm F của cạnh AB, song song với BD và SA là hình gì?
A. Lục giác
B. Tam giác
C. Tứ giác
D. Ngũ giác
Đáp án D
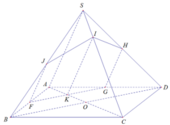
Trong (ABCD), kẻ đường thẳng d đi qua F và song song với BD
d cắt AD tại G
d cắt AC tại K ⇒ F G ∩ A C = K
Trong (SAD), kẻ đường thẳng x đi qua G và song song với SA
x cắt SD tại H
Trong (SAB), kẻ đường thẳng y đi qua F và song song với SA
y cắt SB tại J
Trong (SAC), kẻ đường thẳng z đi qua K và song song với SA
z cắt AC tại I
⇒ FGHIK là thiết diện cần tìm
⇒ thiết diện là ngũ giác
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có
S
A
a
,
S
B
2
a
,
S
C
3
a
và
A
S...
Đọc tiếp
Cho hình chóp S.ABCD có S A = a , S B = 2 a , S C = 3 a và A S B ⏜ = A S C ⏜ = B S C ⏜ = 60 o . Biết đáy ABCD là hình bình hành. Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 2
B. V = a 3 2 2
C. V = a 3 2 3
D. V = 3 a 3 2
Chọn đáp án A
Áp dụng công thức
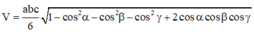
![]()
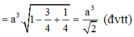
Suy ra V S . A B C D = a 2 2 ( đ v t t )
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a, AD 2a, SA 2a, SA vuông góc với mp(ABCD). Tính thể tích khối chóp S.ABCD. A.
4
a
3
3
(đvtt) B.
4
a
3
(đvtt) C.
2
a
3
3
(đvtt) D.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a, SA = 2a, SA vuông góc với mp(ABCD). Tính thể tích khối chóp S.ABCD.
A. 4 a 3 3 (đvtt)
B. 4 a 3 (đvtt)
C. 2 a 3 3 (đvtt)
D. 2 a 3 (đvtt)
Đáp án A
Ta có:
V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a .2 a = 4 3 a 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD. có đáy ABCD là hình bình hành, E là trung điểm của SA, F, G lần lượt là các điểm thuộc cạnh BC, CD
C
F
F
B
;
G
C
G
D
. Thiết diện của hình chóp cắt bởi
E
F
G...
Đọc tiếp
Cho hình chóp S.ABCD. có đáy ABCD là hình bình hành, E là trung điểm của SA, F, G lần lượt là các điểm thuộc cạnh BC, CD C F < F B ; G C < G D . Thiết diện của hình chóp cắt bởi E F G là
A. Tam giác
B. Tứ giác
C. Ngũ giác
D. Lục giác
Chọn C.
Phương pháp : Dựng thiết diện.
Cách giải : Gọi I, J lần lượt là giao điểm của GF với AB và AD.
Gọi H là giao điểm của IE và SB.
Gọi K là giao điểm của SD và EJ.
Suy ra thiết diện cần tìm là ngũ giác EHFGK.
Đúng 0
Bình luận (0)






