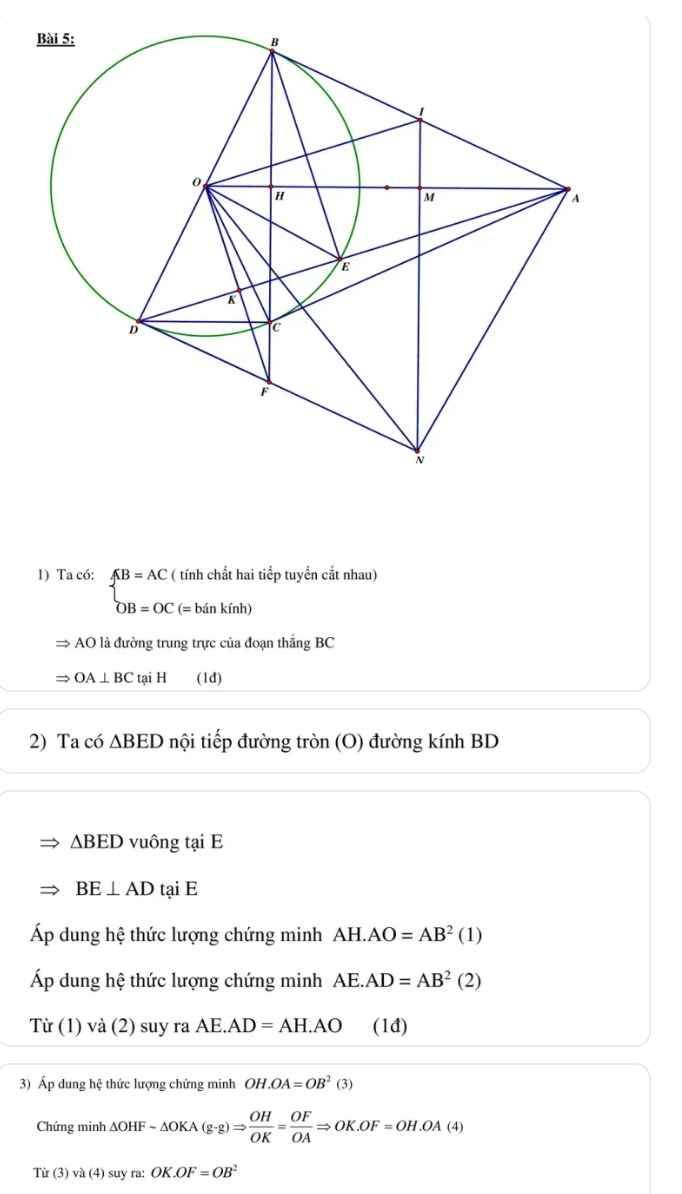
Từ điểm A nằm ngoài đường tròn (O;R) vẽ hai tiếp tuyến AB và AC với đường tròn (O;R) . Gọi H là giao điểm của AO và BC.
a) Chứng minh AO là đường trung trực BC
b) Vẽ đường kính CD của đường tròn (O) , AD cắt đường tròn (O) tại E. Chứng minh \(AB^2=AE.AD\)
c) Tiếp tuyến E của đường tròn (O) cắt AB , AC lần lượt tại M và N . Chứng minh chu vi \(\Delta ANM=AB+AC\)
d) MN cắt AO tại I , EO cắt BC tại P . Chứng minh \(AE//IP\)