Trực tâm của Tầm giác ABC vuông tại A là

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Trực tâm của tam giác ABC là điểm
A. Nằm bên trong tam giác
B. Nằm bên ngoài tam giác
C. Là trung điểm của cạnh huyền BC
D. Trùng với điểm A
Cho tam giác ABC vuông tại A. Khi đó trực tâm tam giác ABC là:
A. Điểm A
B. Điểm B
C. Điểm C
D. Không xác định được
Cho tam giác ABC vuông tại A. Khi đó trực tâm tam giấc ABC là:
A. Điểm C
B. Điểm B
C. Điểm A
D. Không xác định
Cho tam giác ABC vuông tại A. Khi đó trực tâm tam giấc ABC là:
A. Điểm C
B. Điểm B
C. Điểm A
D. Không xác định
Cho tam giác ABC vuông tại B. Điểm nào là trực tâm của tam giác đó?
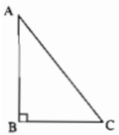
Vì tam giác ABC vuông tại B nên AB ⊥ BC.
Suy ra AB là đường cao kẻ từ đỉnh A và CB là đường cao kẻ từ đỉnh C.
Vì B là giao điểm của 2 đường cao AB và CB nên B là trực tâm của tam giác ABC.
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A trung yến BB' và CC' cắt nhau tại M ,BH vuông góc CC' , CK vuông góc BB' , BH cát CK tại D chứng minh a, tam giác BHC = tam giác CKB b, tam giác HMK cân , HK // BC c, Trọng tâm của tam giác ABC đống thời là trực tâm của tam giác BDC
Xem chi tiết
Cho tam giác ABC vuông tại A trung tuyến BM.Gọi O là giao điểm các đường trung trực của tam giác ABC. E là trọng tâm của tam giác ABM.Chứng minh EO vuông góc với BM
Cho tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của tam giác ABC, AHB, AHC.
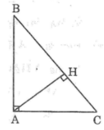
*Tam giác ABC có ∠(BAC) = 90o
Vì CA là đường cao xuất phát từ đỉnh C; BA là đường cao xuất phát từ đỉnh B
Và hai đường cao này cắt nhau tại A nên A là trực tâm của ΔABC.
*Tam giác AHB có ∠(AHB) = 90o
Vì AH là đường cao xuất phát từ đỉnh A, BH là đường cao xuất phát từ đỉnh B và giao điểm của hai đường này là H.
Vậy H là trực tâm của ΔAHB.
*Tam giác AHC có ∠(AHC) = 90o
Vì AH là đường cao xuất phát từ đỉnh A, CH là đường cao xuất phát từ đỉnh C và giao điểm của hai đường này là H.
Vậy H là trực tâm của ΔAHC.
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a có góc a nhọn. gọi h là trực tâm của tâm giác và góc hba=30 độ. Xét 2 khẳng định sau:
A. tam giác ABC vuông cân
B. tam giác ABC đều
giải thịch và chọn đáp án đúng
a: Vì góc A nhọn nên chắc chắn tam giác ABC không thể vuông cân
=> Loại
b: Gọi giao điểm của BH và AC là K
=> BK\(\perp\)AC tại K
Ta có: ΔABK vuông tại K
nên \(\widehat{ABK}+\widehat{BAK}=90^0\)
hay \(\widehat{BAC}=60^0\)
Xét ΔABC cân tại A có \(\widehat{BAC}=60^0\)
nên ΔABC đều
Đúng 1
Bình luận (2)








