Cho a,b,c là số thực,a+b+c=3,d+e+f=3.ad+be+cf=3.Cmr a+b+c+d+e+f
Những câu hỏi liên quan
Cho a,b,c là số thực,a+b+c=3,d+e+f=3.ad+be+cf=3.Cmr a+b+c+d+e+f
Cho tam giác ABC vuông tại A,AB nhỏ hơn AC,phân giác góc B cắt AC tại D ,trên cạnh BC vafBD lấy điểm E sao cho BE=AB
a,cmr DE vuông góc với BC và BD là trung trực của AE
b,Trên tia đối của tia AB lấy F sao cho AF=CE.cmr 3 điểm E ,D,F thẳng hàng
c,cmr CF//AE
d,cmr AD//DC
GIÚP MÌNH NHÉ !! CÂU C,D THÔI CŨNG ĐC
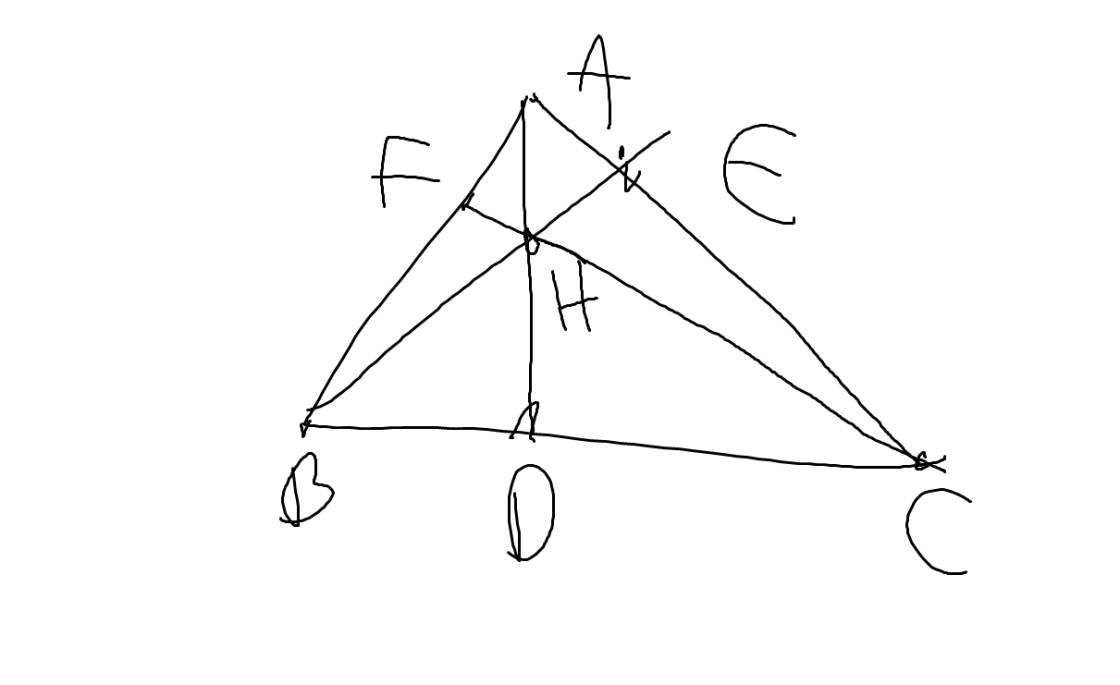
cho Tam giác nhọn ABC, kẻ các đường cao AD,BÉ,CF Cm:4 điểm thuộc một đường tròn: 1) A,F,D,C 2)A,E,D,B 3) gọi H là giải điểm của 3 đường cao Cm: A,F,H,E 4) E,H,D,C 5) E,H,D,B (Vẽ thêm hình càng tốt ạ)
1: Xét tứ giác AFDC có
\(\widehat{AFC}=\widehat{ADC}=90^0\)
nên AFDC là tứ giác nội tiếp
2: Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
nên AEDB là tứ giác nội tiếp
3:
Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
=>AEHF là tứ giác nội tiếp
4: Xét tứ giác HECD có
\(\widehat{HEC}+\widehat{HDC}=90^0+90^0=180^0\)
=>HECD là tứ giác nội tiếp
Đúng 2
Bình luận (2)
Cho ABC. AD, BE, CF là 3 đường trung tuyến. Đường thẳng qua E song song với AB và đường thẳng qua F song song với BE cắt nhau tại G. Chứng minh:
a) Tứ giác AFEG là hình bình hành
b) 3 điểm D; E; G thẳng hàng
c) CG = AD
\(a,\left\{{}\begin{matrix}BF//GE\left(gt\right)\\FG//BE\left(gt\right)\end{matrix}\right.\Rightarrow BFGE\) là hbh \(\Rightarrow BF=GE\)
Mà \(BF=AF\left(F.là.trung.điểm.AB\right)\Rightarrow AF=GE\)
Mà \(AF//GE(BF//GE)\)
Do đó \(AFEG\) là hbh
\(b,\left\{{}\begin{matrix}BD=DC\\AE=EC\end{matrix}\right.\Rightarrow ED\) là đtb tg ABC \(\Rightarrow ED//AB\)
Mà \(EG//AB\left(gt\right)\)
Theo tiên đề Ơ-clít ta được EG trùng ED hay E,G,D thẳng hàng
\(c,\) ED là đtb tg ABC nên \(ED=\dfrac{1}{2}AB=AF=BF=GE\left(cm.trên\right)\)
Do đó E là trung điểm GD
Mà E là trung điểm AC nên ADCG là hbh
Do đó \(CG=AD\)
Đúng 3
Bình luận (0)
Bài 1: tìm 3 số a, b, c biết a-b+c 50, a và b tỉ lệ thuận với 2 và 3, c tỉ lệ nghịch với 4 và 3Bài 2: tìm 3 số a, b, c biết 2a+3b-4c 100, a và b tỉ lệ nghịch với 3 và 2, b và c tỉ lệ nghịch với 3 và 2Bài 3: cho tam giác ABC vuông tại A, góc B 45o. Vẽ tia phân giác AD. Trên tia đối của tia AD lấy điểm E sao cho AEBC. Trên tia đối của tia CA lấy điểm F sao cho CFAB. Chứng minh: BEBF, BE vuông góc BFBài 4: Cho đoạn thẳng AB và điểm O là trung điểm của đoạn thẳng đó. Trên nửa mặt phẳng đối nhau bờ A...
Đọc tiếp
Bài 1: tìm 3 số a, b, c biết a-b+c= 50, a và b tỉ lệ thuận với 2 và 3, c tỉ lệ nghịch với 4 và 3
Bài 2: tìm 3 số a, b, c biết 2a+3b-4c= 100, a và b tỉ lệ nghịch với 3 và 2, b và c tỉ lệ nghịch với 3 và 2
Bài 3: cho tam giác ABC vuông tại A, góc B= 45o. Vẽ tia phân giác AD. Trên tia đối của tia AD lấy điểm E sao cho AE=BC. Trên tia đối của tia CA lấy điểm F sao cho CF=AB. Chứng minh: BE=BF, BE vuông góc BF
Bài 4: Cho đoạn thẳng AB và điểm O là trung điểm của đoạn thẳng đó. Trên nửa mặt phẳng đối nhau bờ AB, kẻ 2 tia Ax, By sao cho Ax song song với By. Trên tia Ax lấy điểm C và E( E nằm giữa A và C), trên tia By lấy điểm D và F sao cho BD=AC, BF=AC. Chứng minh:
a) 3 điểm C, O, D thẳng hàng và E, O, F thẳng hàng
b) DE= CF và DE song song CF
Cho 6điểm A,B,C,D,E,F .CMR
A, vector AD + vector BE + vectơ CF = vector AE+ Vectơ BF+ Vectơ CD = vector AF + VECTO BD + vectơ CE
Cho tam giác ABC vuông tại A, AB=c, AC=b, BC=a, AD vuông góc với BC ở D; DE vuông góc với AB ở E, DF vuong góc với AC tại F. BE=m, CF=n, AD=h. CMR: a.m.n=h3
Xét tam giác vuông ABC, theo hệ thức lượng: \(BD=\frac{c^2}{a}.\)
Xét tam giác vuông BDA, ta có: \(m=EB=\frac{BD^2}{BA}=\frac{c^3}{a^2}\)
Hoàn toàn tương tự: \(n=\frac{b^3}{a^2}\)
Vậy thì \(a.m.n=\frac{b^3.c^3}{a^3}\)
Lại có: \(bc=ah\Rightarrow\frac{bc}{a}=h\Rightarrow\frac{b^3c^3}{a^3}=h^3\Rightarrow a.m.n=h^3.\)
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A, đường cao AD. Biết BC = a, AC =b, AB = c và AD = h
a) CMR: Số đo đọ dài của h; b+c và a+h là số đo 3 cạnh của một tam giác vuông.
b) Kẻ DE⊥ AB tại E; DF⊥ AC tại F.
CMR: AE=\(\frac{b^2c}{b^2+c^2}\) và AF= \(\frac{bc^2}{b^2+c^2}\)
c) CMR: \(\frac{BE}{CF}=\frac{c^3}{b^3}\)
Cho tam giác ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H ( D,E,F lần lượt thuộc các cạnh BC, CA, AB). CMR:a, AF.AB AH.AD AE.ACb, H là giao điểm 3 đường phân giác trong tam giác DEF.c, Gọi M,N,P,I,K,Q lần lượt là trung điểm của các cạnh BC, AC, AB, EF, ED, DF. CMR:các đường thẳng MI, NQ, PK đồng quyd, Gọi độ dài các đoạn thẳng AB, BC, CA lần lượt là a,b,c. Độ dài các đoạn thẳng AD, BE, CF là a, b, c. Tìm GTNN của biểu thức frac{left(a+b+cright)^2}{a^2+b^2+c^2}
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn. Các đường cao AD, BE, CF cắt nhau tại H ( D,E,F lần lượt thuộc các cạnh BC, CA, AB). CMR:
a, AF.AB = AH.AD = AE.AC
b, H là giao điểm 3 đường phân giác trong tam giác DEF.
c, Gọi M,N,P,I,K,Q lần lượt là trung điểm của các cạnh BC, AC, AB, EF, ED, DF. CMR:
các đường thẳng MI, NQ, PK đồng quy
d, Gọi độ dài các đoạn thẳng AB, BC, CA lần lượt là a,b,c. Độ dài các đoạn thẳng AD, BE, CF là a', b', c'. Tìm GTNN của biểu thức \(\frac{\left(a+b+c\right)^2}{a'^2+b'^2+c'^2}\)
Bạn vẽ hình đi mình giải cho