CMR nếu hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau

Những câu hỏi liên quan
Chứng minh rằng nếu hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau
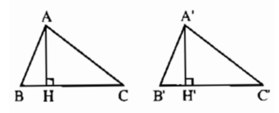
Xét các tam giác bằng nhau ΔABC = ΔA'B'C'. Kẻ AH ⊥ BC, A’H’ ⊥ B’C’
Suy ra ΔABC = ΔA'B'C' nên AC = A’C’, ∠C = ∠C'.
Suy ra ΔAHC = ΔA'H'C' (cạnh – huyền – góc nhọn) nên AH = A’H’.
Đúng 0
Bình luận (0)
câu 1 :đúng hay sai
a)hai tam giác bằng nhau thì hai đường trung tuyến tương ứng bằng nhau
b)hai tam giác bằng nhau thì hai đường phân giác tương ứng bằng nhau
c)hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau
d)trong tam giác cân đường trung tuyến xuất phát từ đỉnh đồng thời là đường phân giác , đường cao, đường trung trực
Chứng minh rằng nếu hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau ?

Xét các tam giác bằng nhau \(\Delta ABC=\Delta A'B'C'\).Kẻ \(AH\perp BC,A'H'\perp B'C'\)(hình bs 16)
Suy ra \(\Delta ABC=\Delta A'B'C'\) nên AC=A'C',\(\widehat{C}=\widehat{C'}\)
Suy ra\(\Delta AHC=\Delta A'H'C'\)(cạnh huyền -góc nhọn) nên AH=A'H'
Đúng 0
Bình luận (0)
CMR: nếu một tam giác có hai cạnh không bằng nhau, thì tổng của cạnh lớn hơn và đường cao tương ứng lớn hơn tổng của cạnh nhỏ hơn và đường cao tương ứng
Chứng minh rằng nếu hai tam giác bằng nhau thì hai đường phân giác tương ứng cũng bằng nhau
theo giả thiết \(\Delta ABC=\Delta EFG\)\(=>\) góc ABH=góc EFI
và AB=EF
có \(\left\{{}\begin{matrix}AH\\EI\end{matrix}\right.\) là các đường phân giác tương ứng
=>góc BAH= góc FEI
xét tam giác ABH và tam giác EFI có:
góc BAH=góc FEI
AB=EF
góc ABH=góc EFI=>tam giác ABH=tam giác EFI(g.c.c)
=>AH=EI(dpcm)
Đúng 1
Bình luận (0)
Chứng minh rằng nếu hai tam giác bằng nhau thì hai đườg cao tương ứng bằng nhau
Gọi đường cao của tam giác ABC là AH;đường cao của tam giác A'B'C' là A'H'
Xét ta được tam giác AHC=tam giác A'H'C'(cạnh huyền- góc nhọn)
Đúng 0
Bình luận (0)
Đúng ghi Đ, sai ghi S:
a) Nếu hai hình tam giác có đáy bằng nhau thì diện tích của chúng tỉ lệ thuận với chiều caao tương ứng.
b) Nếu hai hình tam giác có chiều cao bằng nhau thì diện tích tỉ lệ thuận với đấy tương ứng.
c) Nếu diện tích tam giác không thay đổi thì đáy của chúng tỉ lệ nghịch với chiều cao tương ứng.
Hai tam giác có hai đường cao thì:
A. Diện tích của chúng bằng nhau
B. Hai tam giác đó bằng nhau
C . Tỉ số diện tích của hai tam giác đó bằng tỉ số của hai cạnh tương ứng với các chiều cao đó
CMR nếu một tam giác có 2 cạnh không bằng nhau thì tổng của cạnh lớn hơn và đường cao tương ứng lớn hơn tổng của cạnh nhỏ hơn và đường cao tương ứng.



















