Từ công thức 4.2 và 4.3 hãy suy ra công thức 4.4
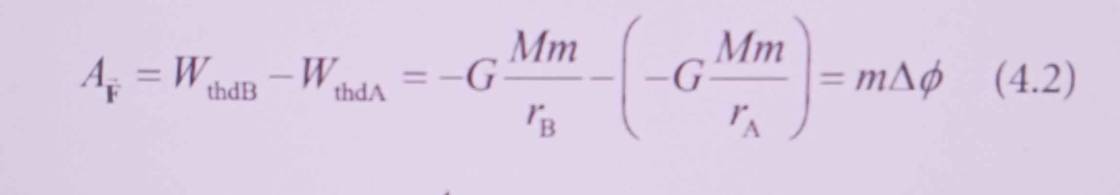
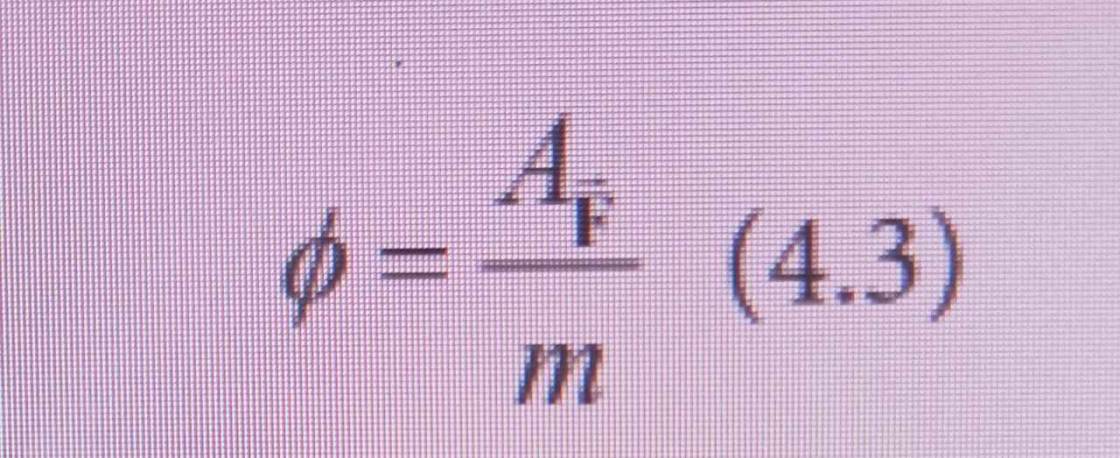
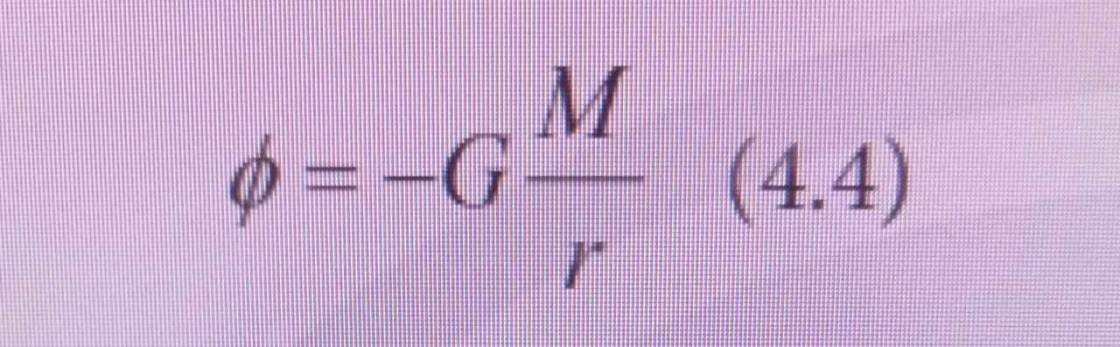
Từ công thức 4.2 và 4.3 hãy suy ra công thức 4.4
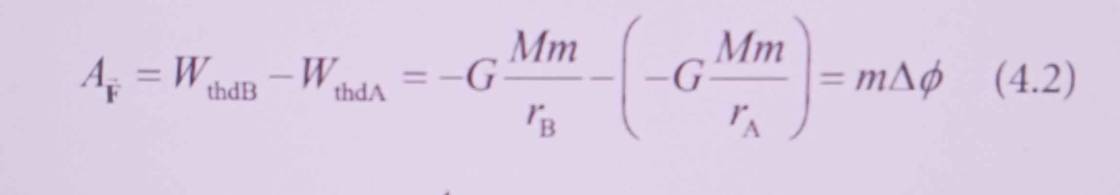
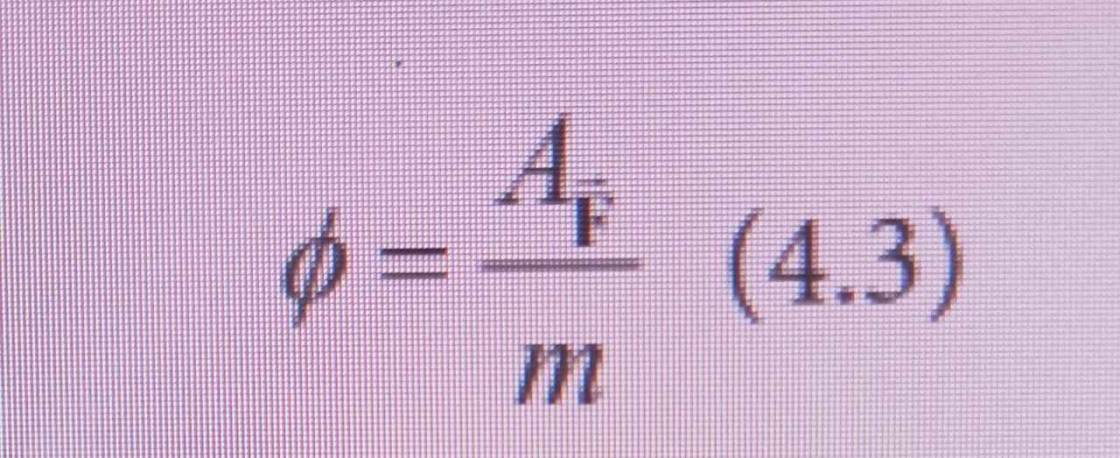
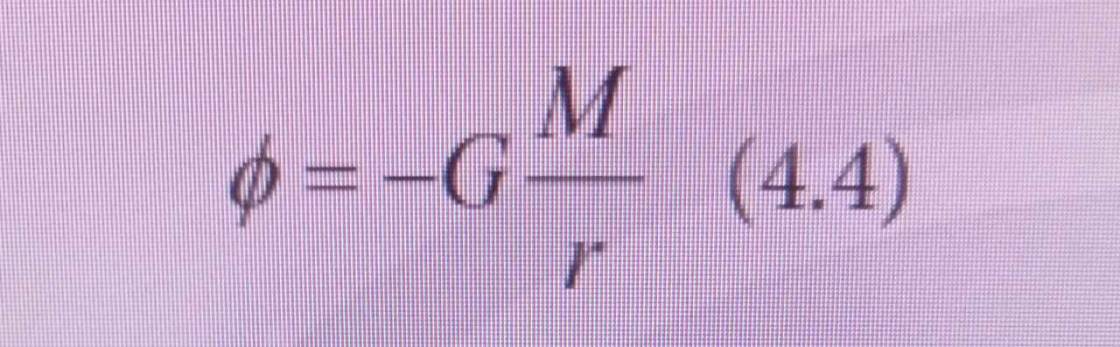
Ta có: Năng lượng thế tại điểm A là: \(W_{thdA}=-G\cdot\dfrac{M\cdot m}{r_A}\)
Và năng lượng thế tại điểm B là: \(W_{thdB}=-G\cdot\dfrac{M\cdot m}{r_B}\)
Hiệu của hai năng lượng thế là:
\(A_{\overrightarrow{F}}=W_{thdB}-W_{thdA}=-G\cdot\dfrac{M\cdot m}{r_B}-\left(-G\cdot\dfrac{M\cdot m}{r_A}\right)=-G\cdot Mm\cdot\left(\dfrac{1}{r_B}-\dfrac{1}{r_A}\right)\)
\(\Rightarrow-G\cdot M\cdot\left(\dfrac{1}{r_B}-\dfrac{1}{r_A}\right)=\dfrac{A_{\overrightarrow{F}}}{m}\left(1\right)\)
Mặt khác: \(\phi=\dfrac{A_{\overrightarrow{F}}}{m}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) ta suy ra: \(\phi=-G\cdot M\cdot\left(\dfrac{1}{r_B}-\dfrac{1}{r_A}\right)=-G\cdot\dfrac{M}{r}\)
Từ công thức tính tần số hãy suy ra công thức tính số dao động và thời gia
\(Hz=\) số lần vật đó dao đông : t
\(t=\dfrac{s}{v}\)
Từ các công thức cộng, hãy suy ra các công thức trên.
+) Từ : cos(a - b)= cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
⇒ cos(a - b) + cos(a + b)= 2cosa cosb
⇒ cosa cosb = 1/2 [cos(a - b) + cos(a + b)]
+) Tương tự: cos(a - b)- cos(a + b) = 2sina sinb
⇒ sinasinb = 1/2 [cos(a - b) - cos(a + b) ]
+) Từ: sin(a - b) = sina cosb - cosa sinb
sin(a + b)= sina cosb + cosa sinb
⇒ sin(a - b) + sin (a + b) = 2 sina cosb
⇒ sina cosb = 1/2 [sin(a - b)+ sin(a + b)]
Từ công thức tính diện tích hình chữ nhật hãy suy ra công thức tính diện tích hình vuông, tam giác vuông.
- Diện tích hình vuông cạnh a: S = a2
- Diện tích tam giác vuông có hai cạnh góc vuông a và b là: S = 0,5 ab
4.3+4.2+5.5+4.4=?
Từ định luật Húc về biến dạng cơ của vật rắn, hãy suy ra công thức của lực đàn hồi trong vật rắn.
Trong giới hạn đàn hồi, độ biến dạng tỉ đối của vật rắn hình trụ tỉ lệ với ứng suất gây ra nó: 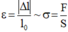
Có thể viết:  là hệ số tỉ lệ (E là suất đàn hồi đơn vị là Pa)
là hệ số tỉ lệ (E là suất đàn hồi đơn vị là Pa)
Suy ra: 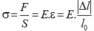
(E là suất đàn hồi, đơn vị là Pa ; S: Diện tích tiết diện của vật rắn đồng chất, hình trụ. lo: Chiều dài ban đầu của vật).
Chú ý: Với 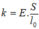 là hệ số đàn hồi hay độ cứng của thanh rắn, thì lực đàn hồi tính theo biểu thức:
là hệ số đàn hồi hay độ cứng của thanh rắn, thì lực đàn hồi tính theo biểu thức: 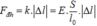
Một nguyên tử có cấu hình electron 1s22s22p3.
a. Xác định vị trí của nguyên tố đó trong bảng tuần hoàn, suy ra công thức phân từ hợp chất khí với hidro.
b. Viết công thức electron và công thức cấu tạo của phân tử đó.
Tham khảo:
a) Tổng số electron là 7, suy ra số thứ tự của nguyên tố là 7. Có 2 lớp electron suy ra nguyên tố ở chu kì 2. Nguyên tố p có 5 electron ở lớp ngoài cùng nên thuộc nhóm VA. Đó là nitơ. Công thức phân tử hợp chất với hidro là NH3.
Từ định luật Húc về biến dạng cơ của vật rắn, hãy suy ra công thức của lực đàn hồi trong vật rắn.
Hướng dẫn giải:
Trong giới hạn đàn hổi, độ biến dạng tỉ đối của thanh rắn tỉ lệ thuận với ứng suất của lực kéo thanh đó:
\(\dfrac{\Delta l}{l_0}=\alpha\sigma\)
với α là hệ số tỉ lệ phụ thuộc chấ liệu của thanh rắn.
Lực đàn hồi Fđh tỉ lệ với độ biến dạng ∆l = |l – l0| của thanh rắn:
\(F_{đh}=k\Delta l\) với \(k=E\dfrac{S}{l_0}\)
Trong đó:
\(E=\dfrac{1}{a}=\) suất đàn hồi đặc trưng cho tính đàn hồi của thanh rắn.
Đơn vị của E là paxcan (Pa).
k = độ cứng của thanh rắn phụ thuộc chất liệu và kích thước cuả thanh.
Đơn vị đo của k là N/m
Chứng minh công thức tính diện tích tổng quát của đa giác đều có số cạnh là n. Từ đó suy ra công thức tính diện tích hình tròn.