Tìm dùm em 1 người dũng cảm,tài năng,sáng tạo với ạ ,em cảm ơn .

Những câu hỏi liên quan
ai là CTV xóa dùm em hết câu hỏi trong tài khoản này với ạ :((( em cảm ơn
ủa sao lại xóa:)??
Mà CTV ko rảnh đâu nên đừng nhờ nha!
Đúng 0
Bình luận (2)
tìm số tự nhiên x
(1/2 +1/6 +1/12+1/20 +1/30)=x/6
mong mọi người giải nhanh dùm em trong sáng hôm nay ạ . Em cảm ơn!
Ta có:
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+\frac{1}{30}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+\frac{1}{5.6}\)
\(=\frac{2-1}{1.2}+\frac{3-2}{2.3}+\frac{4-3}{3.4}+\frac{5-4}{4.5}+\frac{6-5}{5.6}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}\)
\(=1-\frac{1}{6}=\frac{5}{6}\)
Nên phương trình ban đầu tương đương với:
\(\frac{5}{6}=\frac{x}{6}\Leftrightarrow x=5\)
mọi người ai làm gấp dùm em câu này với em cảm ơn ạ!
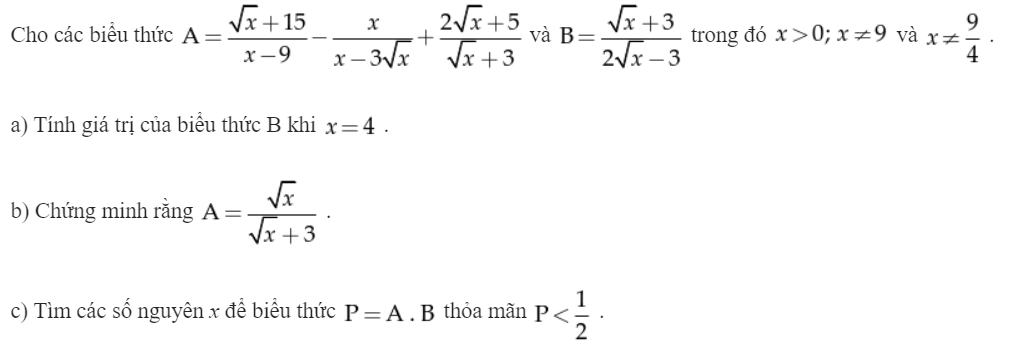
\(a,B=\dfrac{2+3}{2.2+3}=\dfrac{5}{7}\\ b,A=\dfrac{\sqrt{x}+15-x-3\sqrt{x}+2x-\sqrt{x}-15}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ A=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+3}\\ c,P=AB=\dfrac{\sqrt{x}}{2\sqrt{x}-3}< \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}}{2\sqrt{x}-3}-\dfrac{1}{2}< 0\\ \Leftrightarrow\dfrac{2\sqrt{x}-2\sqrt{x}+3}{2\left(2\sqrt{x}-3\right)}< 0\Leftrightarrow\dfrac{3}{2\left(2\sqrt{x}-3\right)}< 0\\ \Leftrightarrow2\sqrt{x}-3< 0\left(3>0\right)\\ \Leftrightarrow\sqrt{x}< \dfrac{3}{2}\Leftrightarrow0< x< \dfrac{9}{4}\)
Đúng 0
Bình luận (0)
mọi người giải dùm em vs ạ bạn em nhờ em hỏi dùm
em cảm ơn nhiều
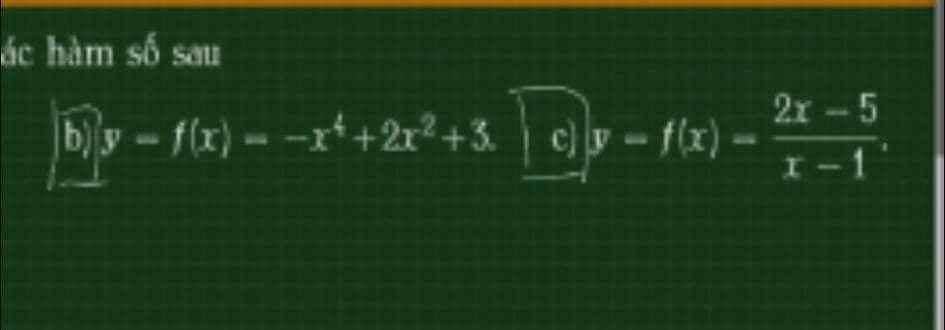

cái hồi nãy thiếu câu hỏi em bổ sung ở dưới này ạ
em cảm ơn mn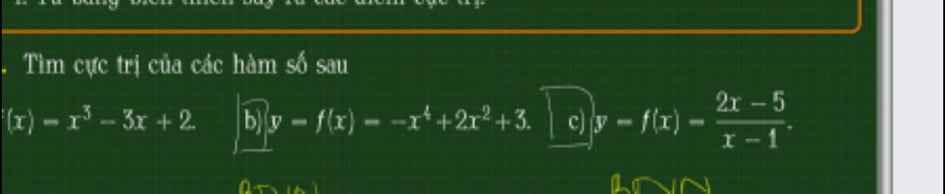
Đúng 0
Bình luận (1)
5.
TXĐ: \(D=\left(-\infty;-1\right)\cup\left(-1;+\infty\right)\)
\(y'=\dfrac{2}{\left(x+1\right)^2}>0\) ; \(\forall x\in D\)
\(\Rightarrow\) Hàm đồng biến trên mỗi khoảng xác định
Hay hàm đồng biến trên \(\left(-\infty;-1\right)\) và \(\left(-1;+\infty\right)\)
6.
\(y=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
Dấu của y' trên trục số:
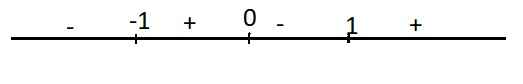
Từ đó ta thấy:
Hàm đồng biến trên các khoảng \(\left(-1;0\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Đúng 0
Bình luận (0)
Tìm cực trị
a.
\(f'\left(x\right)=3x^2-3=0\Rightarrow x=\pm1\)
\(f''\left(x\right)=6x\)
\(f''\left(-1\right)=-6< 0\)
\(f''\left(1\right)=6>0\)
\(\Rightarrow x=-1\) là điểm cực đại và \(x=1\) là điểm cực tiểu
b.
\(f'\left(x\right)=-4x^3+4x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=1\end{matrix}\right.\)
\(f''\left(x\right)=-12x^2+4\)
\(f''\left(0\right)=4>0\) ; \(f''\left(-1\right)=-8< 0\) ; \(f''\left(1\right)=-8< 0\)
\(\Rightarrow x=0\) là điểm cực tiểu và \(x=\pm1\) là 2 điểm cực đại
c.
\(f'\left(x\right)=\dfrac{3}{\left(x-1\right)^2}\ne0\) với mọi x thuộc miền xác định
Hàm không có cực trị
Đúng 0
Bình luận (0)
Có ý kiến cho rằng sáng tạo là phẩm chất của thiên tài? Em hãy làm sáng tỏ ý kiến trên.
giải giúp mik vs ạ
chìu mik thi rùi ! cảm ơn nhìu
Cấu tạo và chức năng của rễ co hút. Giúp em với ạ, em cảm ơn
Em check lại kĩ xem nội dung câu hỏi đúng chưa em hấy
Đúng 1
Bình luận (0)
Giải dùm em hết với ạ,em đang cần qấp, em cảm ơn ạ !

giải dùm em cái này vs ạ
em cảm ơn mọi người nhiều
mọi người giải giúp em câu 71,74 với
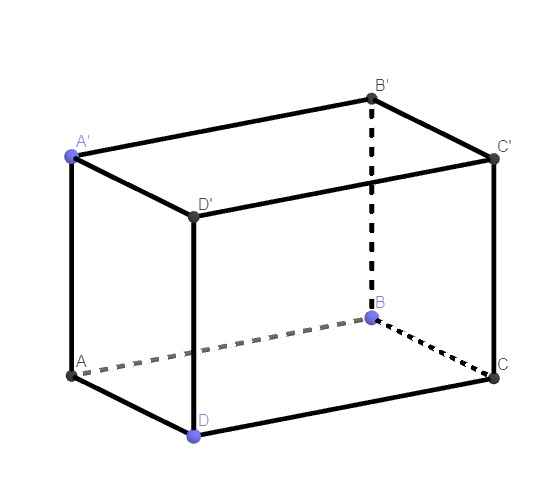
em cảm ơn mọi người nhiều vẽ hình dùm em luôn em cảm ơn
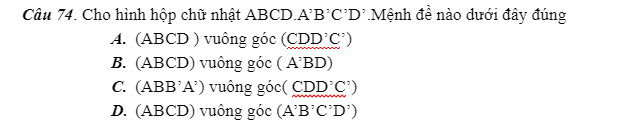
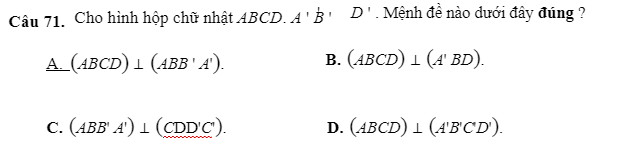
71.
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)
Đúng 0
Bình luận (0)















