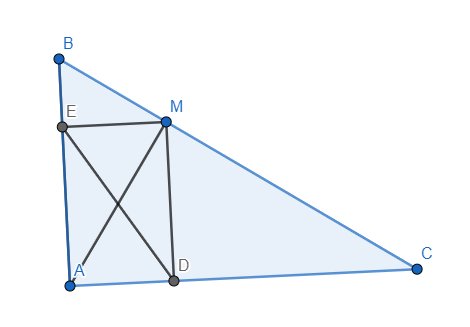
Do MD//AB và \(AB\perp AD\) nên \(MD\perp AD\) hay \(\widehat{ADM}=90^o\). Hoàn toàn tương tự, ta có \(\widehat{AEM}=90^o\). Mà \(\widehat{DAE}=90^o\) nên tứ giác ADME là hình chữ nhật. Do đó \(DE=AM\). Như vậy, ta quy về tìm vị trí của M trên BC để AM nhỏ nhất. Kẻ đường cao AH của tam giác ABC thì H cố định. Ta thấy AH và AM lần lượt là đường vuông góc và đường xiên kẻ từ A lên BC nên \(AM\ge AH\). Dấu "=" chỉ xảy ra khi \(M\equiv H\) hay M là chân đường vuông góc hạ từ A lên BC. 

Đáp án D

Gọi G  là trọng tâm tam giác ABC. 

Ta có 

Gọi G  là trọng tâm tam giác ABC.

Ta có

Chọn D.

Bài 1:

Gọi K là trung điểm của BC

ABCD là hình bình hành

=>AC cắt BD tại trung điểm của mỗi đường

=>O là trung điểm chung của AC và BD

Xét ΔCAB có

O,K lần lượt là trung điểm của CA,CB

=>OK là đường trung bình

=>OK//AB và \(OK=\dfrac{AB}{2}\)

=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)

=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)

Xét ΔOBC có OK là đường trung tuyến

nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)

=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)

=>M trùng với B

Bài 2:

Xét ΔABC có

M,P lần lượt là trung điểm của AB,AC

=>MP là đường trung bình của ΔABC

=>MP//BC và MP=BC/2

=>MP=CN

mà MP//NC

nên MPCN là hình bình hành

=>\(\overrightarrow{MP}=\overrightarrow{NC}\)

=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)

=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)

mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)

nên K trùng với P

Vẽ MH ^ BC, BK ^ AC.

S_AMNB = 3S_MNC

Þ S_ABC = 4S_MNC

Ta có: S A B C S B M C = A C M C = 3 2  

S B M C S M N C = B C N C = 6 N C ⇒ S A B C S M N C = 9 N C  

Mà S_ABC = 4S_CMN Þ NC = 2,25