Từ đồ thị vận tốc – thời gian của chuyển động thẳng biến đổi đều mô tả được chuyển động này.

Những câu hỏi liên quan
phân tích mối liên hệ về kiến thức giữa mấy bài dưới đây giúp e với. e chân thành cảm ơn.Bài 2. VẬN TỐC TRONG CHUYỂN ĐỘNG THẲNGCHUYỂN ĐỘNG THẲNG ĐỀU (Tiêt 1)- Hiểu rõ được các khái niện vectơ độ dời, vectơ vận tốc trung bình, vectơ vận tốc tức thời.- Hiểu được việc thay thế các vectơ trên bằng các giá trị đại số của chúng không làm mất đi đặc trưng của vectơ của chúng.- phân biệt được độ dời với quãng đường đi, vận tốc với tốc độ.Bài 3. VẬN TỐC TRONG CHUYỂN ĐỘNG THẲNG ...
Đọc tiếp
phân tích mối liên hệ về kiến thức giữa mấy bài dưới đây giúp e với. e chân thành cảm ơn.
Bài 2. VẬN TỐC TRONG CHUYỂN ĐỘNG THẲNG
CHUYỂN ĐỘNG THẲNG ĐỀU (Tiêt 1)
- Hiểu rõ được các khái niện vectơ độ dời, vectơ vận tốc trung bình, vectơ vận tốc tức thời.
- Hiểu được việc thay thế các vectơ trên bằng các giá trị đại số của chúng không làm mất đi đặc trưng của vectơ của chúng.
- phân biệt được độ dời với quãng đường đi, vận tốc với tốc độ.
Bài 3. VẬN TỐC TRONG CHUYỂN ĐỘNG THẲNG
CHUYỂN ĐỘNG THẲNG ĐỀU (Tiết 2)
- Biết cách thiết lập phương trình chuyển động thẳng đều. Hiểu được phương trình chuyển động mô tả đầy đủ các đặc tính của chuyển động.
- Biết cách vẽ đồ thị tọa độ theo thời gian, vận tốc theo thời gian và từ đồ thị có thể xác định được các đặc trưng động học của chuyển động
Bài 4. CHUYỂN ĐỘNG THẲNG BIẾN ĐỔI ĐỀU
- Hiểu được gia tốc là đại lượng đặc trưng cho sự biến đổi nhanh, chậm của tốc độ.
- Nắm được các định nghĩa gia tốc trung bình, gia tốc tức thời.
- Hiểu được định nghĩa về chuyển động thẳng biến đổi đều, từ đó rút ra được công thức tính vận tốc theo thời gian.
Câu hỏi kiểu như thế này chắc em phải vẽ sơ đồ tư duy rồi.
Đúng 0
Bình luận (0)
Gửi em một sơ đồ mà mình sưu tầm được trên mạng

Đúng 0
Bình luận (1)
Thế nào là chuyển động thẳng tiến biến đổi đều? Viết công thức tính vận tốc và đồ thị của vận tốc theo thời gian trong chuyển động thẳng biến đổi đều
* Chuyển động thẳng biến đổi đều là chuyển động có quỹ đạo là đường thẳng trong đó độ lớn của vận tốc tức thời hoặc tăng đều hoặc giảm đều theo thời gian.
* Công thức tính vận tốc:
Chọn một chiều dương trên quỹ đạo. Gọi v ; v 0 lần lượt là vận tốc tại các thời điểm t và t 0 , a là gia tốc, ta có công thức: v = v 0 + a t .
- Nếu a cùng dấu với v thì chuyển động là nhanh dần đều.
- Nếu a trái dấu với v thì chuyển động là chậm dần đều.
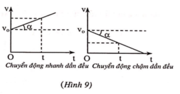
* Đồ thị vận tốc theo thời gian:
Đồ thị của vận tốc theo thời gian t là một đường thẳng cắt trục tung tại điểm v = v 0 (Hình 9)
Hệ số góc của đường thẳng đó bằng gia tốc: = a = tan α = v − v 0 t .
Đúng 0
Bình luận (0)
Xét một vận động viên chạy xe đạp trên một đoạn đường thẳng. Vận tốc của vận động viên này tại mỗi thời điểm được ghi lại trong bảng dưới đây.

Hãy vẽ đồ thị vận tốc – thời gian và mô tả tính chất chuyển động của vận động viên này.
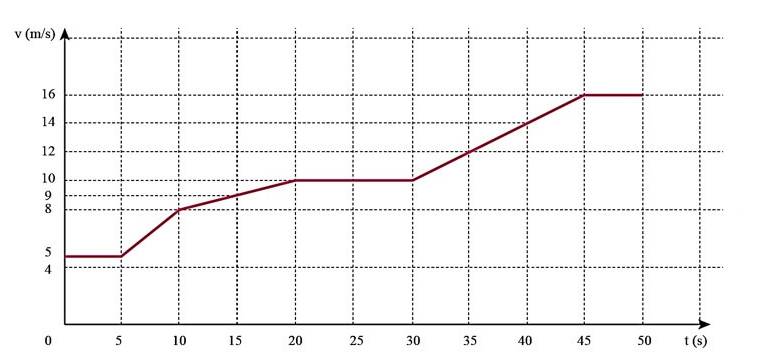
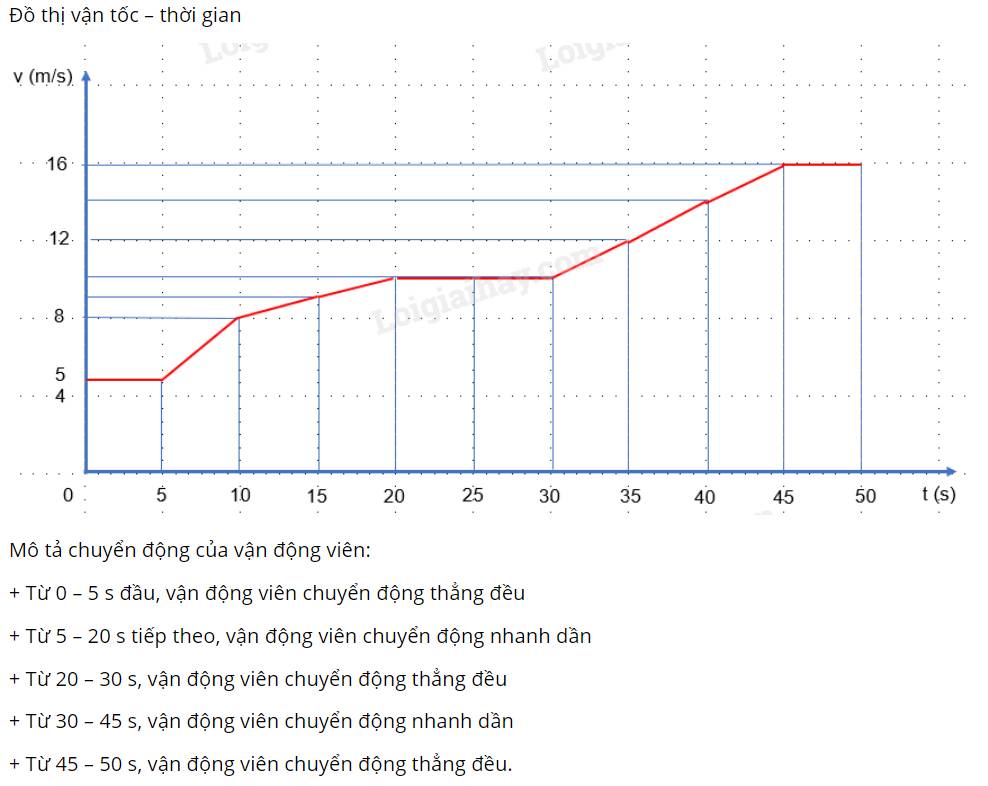
Mô tả chuyển động của vận động viên:
+ Từ 0 – 5 s đầu, vận động viên chuyển động thẳng đều
+ Từ 5 – 20 s tiếp theo, vận động viên chuyển động nhanh dần
+ Từ 20 – 30 s, vận động viên chuyển động thẳng đều
+ Từ 30 – 45 s, vận động viên chuyển động nhanh dần
+ Từ 45 – 50 s, vận động viên chuyển động thẳng đều.
Đúng 0
Bình luận (0)
2. Xét một vận động viên chạy xe đạp trên một đoạn đường thẳng. Vận tốc của vận động viên này tại mỗi thời điểm được ghi lại trong bảng dưới đây.

Hãy vẽ đồ thị vận tốc – thời gian và mô tả tính chất chuyển động của vận động viên này.
Chỉ ra câu sai.A. Vận tốc tức thời của chuyển động thẳng biến đổi đều có độ lớn tăng hoặc giảm đều theo thời gian.B. Gia tốc của chuyển động thẳng biến đổi đều có độ lớn không đổi.C. Vectơ gia tốc của chuyển động thẳng biến đổi đều có thể cùng chiều hoặc ngược chiều với vectơ vận tốc.D. Trong chuyển động thẳng biến đổi đều, quãng đường đi được trong những khoảng thời gian bằng nhau thì bằng nhau.
Đọc tiếp
Chỉ ra câu sai.
A. Vận tốc tức thời của chuyển động thẳng biến đổi đều có độ lớn tăng hoặc giảm đều theo thời gian.
B. Gia tốc của chuyển động thẳng biến đổi đều có độ lớn không đổi.
C. Vectơ gia tốc của chuyển động thẳng biến đổi đều có thể cùng chiều hoặc ngược chiều với vectơ vận tốc.
D. Trong chuyển động thẳng biến đổi đều, quãng đường đi được trong những khoảng thời gian bằng nhau thì bằng nhau.
Một vật chuyển động thẳng biến đổi đều có đồ thị vận tốc v theo thời gian t như hình vẽ. Phương trình vận tốc của vật là: A. v 15 – t(m/s) B. v t + 15(m/s) C. v 10 – 5t(m/s) D. v 10 – 15t(m/s)
Đọc tiếp
Một vật chuyển động thẳng biến đổi đều có đồ thị vận tốc v theo thời gian t như hình vẽ. Phương trình vận tốc của vật là:
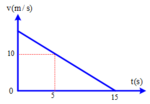
A. v = 15 – t(m/s)
B. v = t + 15(m/s)
C. v = 10 – 5t(m/s)
D. v = 10 – 15t(m/s)
Bài 1:xe mô tô đang chuyển động thẳng đều từ A với vận tốc 30 km/h. Chọn gốc tọa độ tại A.b, Vẽ đồ thị tọa độ- thời gian của chuyển động?
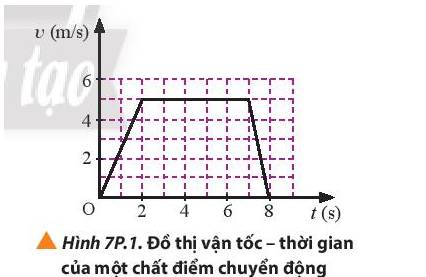
Chất điểm chuyển động có đồ thị vận tốc theo thời gian như hình 7P1
a) Mô tả chuyển động của chất điểm.
b) Tính quãng đường mà chất điểm đi được từ khi bắt đầu chuyển động cho tới khi dừng lại.
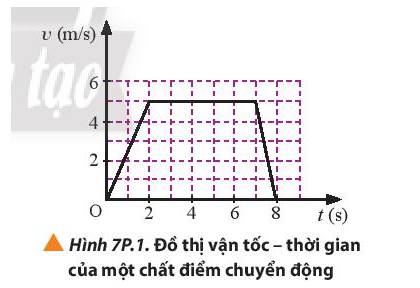
a) Mô tả chuyển động của chất điểm:
+ Từ 0 – 2 s, vật chuyển động thẳng nhanh dần đều
+ Từ 2 – 7 s, vật chuyển động thẳng đều
+ Từ 7 – 8 s, vật chuyển động thẳng chậm dần đều
b) Quãng đường vật đi được trong 2 s đầu là:
\({a_1} = \frac{{5 - 0}}{2} = 2,5(m/{s^2}) \Rightarrow {s_1} = \frac{{{5^2} - {0^2}}}{{2.2}} = 6,25(m)\)
Quãng đường vật đi được từ 2 – 7 s là:
\({s_2} = 5.(7 - 2) = 25(m)\)
Quãng đường vật đi được từ 7 – 8 s là:
\({a_3} = \frac{{0 - 5}}{{8 - 7}} = - 5(m/{s^2}) \Rightarrow {s_3} = \frac{{{0^2} - {5^2}}}{{2.( - 5)}} = 2,5(m)\)
=> Quãng đường mà chất điểm đi được từ lúc bắt đầu đến khi dừng hẳn là:
S = 6,25 + 25 + 2,5 = 33,75 (m)
Đúng 0
Bình luận (0)
4. Chất điểm chuyển động có đồ thị vận tốc theo thời gian như hình 7P1
a) Mô tả chuyển động của chất điểm.
b) Tính quãng đường mà chất điểm đi được từ khi bắt đầu chuyển động cho tới khi dừng lại.