Cho hình thang vuông ABCD vuông góc tại A và D;AB=1/3CD.Kéo dài DA và CB cắt nhau tại M
A,So sánh diện tích hai tam giác ABC và ADC
B,So sánh diện tích hai tam giác ABM và ACM
C,Diện tích hình thang ABCD bằng 64 cm2. Tính diện tích tam giác MBA
Cho hình thang ABCD vuông góc tại A và D . Hai đường chéo vuông góc với nhau tại O. Biết AB =2√13 , OA =6 . Tính diện tích hình thang ABCD
* Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB=\(2\sqrt{13}\), OA=6, tính diện tích hình thang ABCD
Xét tam giác vuông OAB:
\(OB=\sqrt{AB^2-OA^2}=4\)
Áp dụng hệ thức lượng cho tam giác vuông ABD với đường cao AO:
\(AB^2=OB.BD\Rightarrow BD=\dfrac{AB^2}{OB}=13\)
\(\Rightarrow\left\{{}\begin{matrix}OD=BD-OB=9\\AD=\sqrt{BD^2-AB^2}=\sqrt{29}\end{matrix}\right.\)
\(\widehat{BAO}=\widehat{DCO}\left(slt\right)\Rightarrow\Delta_VAOB\sim\Delta_VCOD\) (g.g)
\(\Rightarrow\dfrac{AB}{DC}=\dfrac{OB}{OD}\Rightarrow DC=\dfrac{AB.OD}{OB}=\dfrac{9\sqrt{13}}{2}\)
\(S_{ABCD}=\dfrac{1}{2}AD.\left(AB+CD\right)=\dfrac{1}{2}.\sqrt{29}.\left(2\sqrt{13}+\dfrac{9\sqrt{13}}{2}\right)=...\)
Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB= 2 căn 13, OA=6. Tính diện tích hình thang ABCD.
Cho hình chóp SABCD có SA vuông góc với (ABCD), SA=a\(\sqrt{2}\), đáy abcd là hình thang vuông tại A và D với AB=2a, AD=DC=a. Tính góc giữa (SBC) và (ABCD)
Cho hình thang vuông ABCD vuông góc tại A và D ,AB=1 PHẦN 3 CD . Kéo dài DA và CB cắt nhau tại M . Diện tích hình thang ABCD là 64 cm vuông . tính diện tích tam giác MBA
Cho hình thang vuông ABCD vuông góc tại A và D; AB = 1 3 CD. Kéo dài DA và CB cắt nhau tại M.
c) Diện tích hình thang ABCD bằng 64 cm2.Tính diện tích tam giác MBA .
cho hình thang vuông tại A và D, 2 đường chéo AC và DB cắt nhau và vuông góc tại O, biết AB=2√13, OA=6. Tính diện tích hình thang ABCD
Cho hình chóp SABCD có SA vuông góc với (ABCD), SA=a√22, đáy abcd là hình thang vuông tại A và D với AB=2a, AD=DC=a. Tính góc giữa (SBC) và (SCD)
Cho hình thang vuông ABCD ( ∠ A = ∠ D = 90 0 ) có hai đường chéo AC và BD vuông góc với nhau tại H. Biết HD = 18cm, HB = 8cm, tính diện tích hình thang ABCD
A. 504 c m 2
B. 505 c m 2
C. 506 c m 2
D. 506 c m 2
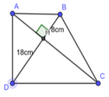
Xét ∆ ADB vuông tại A có: AH là đường cao ứng với cạnh huyền BD
⇒ A H 2 = HB. HD = 8.18 HA = 12 (cm) (hệ thức lượng trong tam giác vuông)
Xét ∆ ADC vuông tại D có: DH là đường cao ứng với cạnh huyền AC
⇒ H D 2 = H A . H C ⇒ 18 2 = 12 H C => HC = 27 (cm) (hệ thức lượng trong tam giác vuông)
Ta có: AC = AH + HC = 12 + 27 = 39 cm
BD = BH + HD = 8 + 18 = 26cm
S A B C D = A C . B D 2 = 26.39 2 = 507 c m 2
Đáp án cần chọn là: D
Các bạn giúp mình bài này với!
Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB= 2 căn 13, OA=6. Tính diện tích hình thang ABCD.
từ tìm dk AD, =>DO
sau đó tìm dk DC=> diện tích hình thang