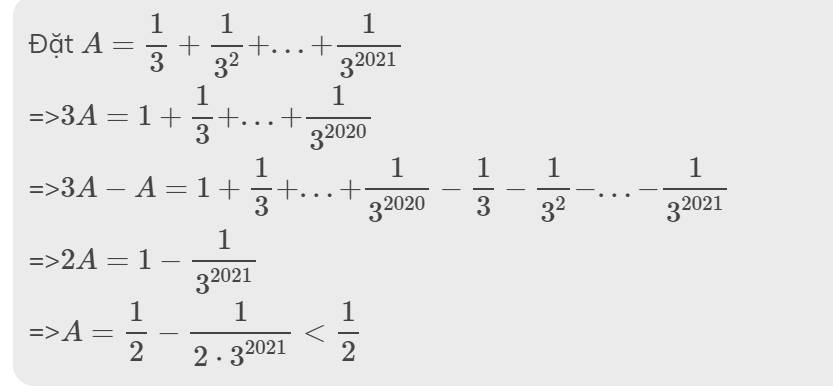
chứng minh rằng: 1/3 + 1/3 mũ 2 + 1/3 mũ 3 + ... + 1/3 mũ 2021<1/2

Những câu hỏi liên quan
chứng minh rằng: 1/3 + 1/3 mũ 2 + 1/3 mũ 3 + ... + 1/3 mũ 2021
Chứng minh rằng: 1/2!+2/3!+3/4!+......+99/100! <1
Thêm câu này nhé!
Chứng minh rằng: Mọi số nguyên dương thì 3 mũ n+2 - 2 mũ n+2 +3 mũ n -2 mũ n chia hết cho 10
M = 1 + 3 + 3 mũ 2 + 3 mũ 3 + 3 mũ 4 + ..... + 3 mũ 2019 + 3 mũ 2020 chứng minh ( M - 1 ) ⋮ 4
https://hoc24.vn/cau-hoi/.2044867324230
làm r
Đúng 2
Bình luận (0)
cho tổng S=1+2+2 mũ 2+2 mũ 3 +......+2 mũ 98+2 mũ 99
chứng tỏ rằng S chia hết cho15
\(S=1+2+2^2+2^3+...+2^{99}\)
\(=\left(1+2+2^2+2^3\right)+...+\left(2^{96}+2^{97}+2^{98}+2^{99}\right)\)
\(=\left(1+2+4+8\right)+...+2^{96}.\left(1+2+2^2+2^3\right)\)
\(=15+...+2^{96}.15\)
\(=15.\left(1+...+2^{96}\right)⋮15\)
\(\Rightarrow\) \(S⋮15\)
Đúng 0
Bình luận (0)
Cho M = 3 MŨ 1 + 3 MŨ 2 + 3 MŨ 3 +......+3 MŨ 28 + 3 MŨ 29 + 3 MŨ 30 .
CHỨNG MINH M CHIA HẾT CHO 3
AI ĐÚNG EM TICK Ạ
M = 3 + 32 + 33 + .... + 328 + 329+ 330
= 3.( 1 + 3 + 32 + ..... + 329)
Vì trong tích có 1 thừa số là 3 nên tích chia hết cho 3
Đúng 1
Bình luận (0)
Vì số 3 mũ bao nhiêu lên cũng chia hết cho 3
mà tổng các số chia hết cho 3 thì chia hết cho 3
Đúng 0
Bình luận (0)
Chuứng tỏ rằng : 1 phần 3 (3 mũ 2) + 1 phần 4 (4 mũ 2) + 1 phần 5 (5 mũ 2) + 1 phần 6 (6 mũ 2) +.........+ 1 phần 100 (100 mũ 2) < 1 phần 2
a) Gọi tổng đó là A \(A = 1/1.2 + 1/2.3 +......+ 1/99.100 \)
A = 1/1.2 + 1/2.3 +......+ 1/99.100
A = 1 - 1/2 + 1/2 - 1/3 +.......+1/99 - 1/100
A = 1 - 1/100
A = 99/100 < 1
=> A < 1 (đpcm)
Gọi tổng trên là B
B = 1/22 + 1/32 +.......+ 1/1002
B = 1/2.2 + 1/3.3 + .......+ 1/100.100
B < 1/1.2 + 1/2.3 +......+ 1/99.100 B < 1 - 1/2 + 1/2 - 1/3 +.......+ 1/99 - 1/100 B < 1 - 1/100
B < 99/100 < 1
=> B < 1 (đpcm)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1) Thực hiện phép tính :
a) -(5x - 4)(2x+3)
b) ( x - y)( x mũ 2 + xy+ y mũ 2)
c) 7x( x - 4) - ( 7x +3)(2x mũ 2 - x+4)
2) Chứng minh rằng giá trị của biểu thức không phụ thuộc vào giá trị của biến x:
a) x(3x +12) - ( 7x - 20) + x(2x - 3) - x( 2x +5)
b) 3( 2x-1) - 5( x-3) + 6( 3x - 4) - 19x
3) tìm x:
a) 3x( x - 2) - x( 1+3x) 14
b) (2x - 1)( x + 5) - (2x +1)( x + 4,5)3,5
c) 3x mũ 2 - 3x( x - 3) 36
d) (3x + 1)(x - 1) + x( 4 - 3x ) 5
4/ Phân tích đa thức thành nhân tử:
a....
Đọc tiếp
1) Thực hiện phép tính :
a) -(5x - 4)(2x+3)
b) ( x - y)( x mũ 2 + xy+ y mũ 2)
c) 7x( x - 4) - ( 7x +3)(2x mũ 2 - x+4)
2) Chứng minh rằng giá trị của biểu thức không phụ thuộc vào giá trị của biến x:
a) x(3x +12) - ( 7x - 20) + x(2x - 3) - x( 2x +5)
b) 3( 2x-1) - 5( x-3) + 6( 3x - 4) - 19x
3) tìm x:
a) 3x( x - 2) - x( 1+3x) = 14
b) (2x - 1)( x + 5) - (2x +1)( x + 4,5)=3,5
c) 3x mũ 2 - 3x( x - 3) = 36
d) (3x + 1)(x - 1) + x( 4 - 3x )= 5
4/ Phân tích đa thức thành nhân tử:
a. 14xy - 21xy - 28xy
b. x( x + y) - 5x - 5y
c. 10x( x - y ) - 8( y - x )
d. x mũ 3 - x + 3x mũ 2 y + 3 xy mũ 2 + y mũ 3 - y
e. x mũ 2 + 7x - 8
f. 2x mũ 2 - 3x - 2
g. - 5x mũ 2 + 16x - 3
h. x mũ 2 - 2xy - 3y mũ 2
i. x mũ 2 - 2xy + y mũ 2 - z mũ 2
Giải hộ mình với ạ ....
Bài 4:
a: \(=7xy\left(2-3-4\right)=-35xy\)
b: \(=\left(x-5\right)\left(x+y\right)\)
c: \(=10x\left(x-y\right)+8\left(x-y\right)=2\left(x-y\right)\left(5x+4\right)\)
d: \(=\left(x+y\right)^3-\left(x+y\right)\)
=(x+y)(x+y+1)(x+y-1)
e: =x^2+8x-x-8
=(x+8)(x-1)
f: \(=2x^2-4x+x-2=\left(x-2\right)\left(2x+1\right)\)
g: =-5x^2+15x+x-3
=(x-3)(-5x+1)
h: =x^2-3xy+xy-3y^2
=x(x-3y)+y(x-3y)
=(x-3y)*(x+y)
Đúng 0
Bình luận (0)
1) Thực hiện phép tính :
a) -(5x - 4)(2x+3)
b) ( x - y)( x mũ 2 + xy+ y mũ 2)
c) 7x( x - 4) - ( 7x +3)(2x mũ 2 - x+4)
2) Chứng minh rằng giá trị của biểu thức không phụ thuộc vào giá trị của biến x:
a) x(3x +12) - ( 7x - 20) + x(2x - 3) - x( 2x +5)
b) 3( 2x-1) - 5( x-3) + 6( 3x - 4) - 19x
3) tìm x:
a) 3x( x - 2) - x( 1+3x) 14
b) (2x - 1)( x + 5) - (2x +1)( x + 4,5)3,5
c) 3x mũ 2 - 3x( x - 3) 36
d) (3x + 1)(x - 1) + x( 4 - 3x ) 5
4/ Phân tích đa thức thành nhân tử:
a....
Đọc tiếp
1) Thực hiện phép tính :
a) -(5x - 4)(2x+3)
b) ( x - y)( x mũ 2 + xy+ y mũ 2)
c) 7x( x - 4) - ( 7x +3)(2x mũ 2 - x+4)
2) Chứng minh rằng giá trị của biểu thức không phụ thuộc vào giá trị của biến x:
a) x(3x +12) - ( 7x - 20) + x(2x - 3) - x( 2x +5)
b) 3( 2x-1) - 5( x-3) + 6( 3x - 4) - 19x
3) tìm x:
a) 3x( x - 2) - x( 1+3x) = 14
b) (2x - 1)( x + 5) - (2x +1)( x + 4,5)=3,5
c) 3x mũ 2 - 3x( x - 3) = 36
d) (3x + 1)(x - 1) + x( 4 - 3x )= 5
4/ Phân tích đa thức thành nhân tử:
a. 14xy - 21xy - 28xy
b. x( x + y) - 5x - 5y
c. 10x( x - y ) - 8( y - x )
d. x mũ 3 - x + 3x mũ 2 y + 3 xy mũ 2 + y mũ 3 - y
e. x mũ 2 + 7x - 8
f. 2x mũ 2 - 3x - 2
g. - 5x mũ 2 + 16x - 3
h. x mũ 2 - 2xy - 3y mũ 2
i. x mũ 2 - 2xy + y mũ 2 - z mũ 2
Giải hộ mình với ạ ....
Bài 4:
a: \(=7xy\left(2-3-4\right)=-35xy\)
b: \(=\left(x-5\right)\left(x+y\right)\)
c: \(=10x\left(x-y\right)+8\left(x-y\right)=2\left(x-y\right)\left(5x+4\right)\)
d: \(=\left(x+y\right)^3-\left(x+y\right)\)
=(x+y)(x+y+1)(x+y-1)
e: =x^2+8x-x-8
=(x+8)(x-1)
f: \(=2x^2-4x+x-2=\left(x-2\right)\left(2x+1\right)\)
g: =-5x^2+15x+x-3
=(x-3)(-5x+1)
h: =x^2-3xy+xy-3y^2
=x(x-3y)+y(x-3y)
=(x-3y)*(x+y)
Đúng 0
Bình luận (0)
Cho A= 2 mũ 1 + 2 mũ 2 + 2 mũ 3 +.........2 mũ 60
Chứng tỏ A:2 ; A:3 ; A:7 ; A:14
Có \(A=2+2^2+2^3+...+2^{60}\)
\(\Rightarrow A=2\left(1+2+...+2^{59}\right)⋮2\)(1)
Lại có : \(A=2+2^2+2^3+...+2^{60}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{59}+2^{60}\right)\)
\(A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{59}\left(1+2\right)\)
\(A=3\left(2+2^3+...+2^{59}\right)⋮3\)(2)
Lại có :\(A=2+2^2+2^3+...+2^{60}\)
\(\Rightarrow A=\left(2+2^2+2^3\right)+...+\left(2^{58}+2^{59}+2^{60}\right)\)
\(A=2\left(1+2+2^2\right)+...+2^{58}\left(1+2+2^2\right)\)
\(A=7\left(2+...+2^{58}\right)⋮7\)(3)
Từ (1) và (3) \(\Rightarrow A⋮\left(2.7\right)=14\)(4)
Từ(1);(2);(3);(4) \(\Rightarrow A⋮2;3;7;14\)
Đúng 0
Bình luận (0)