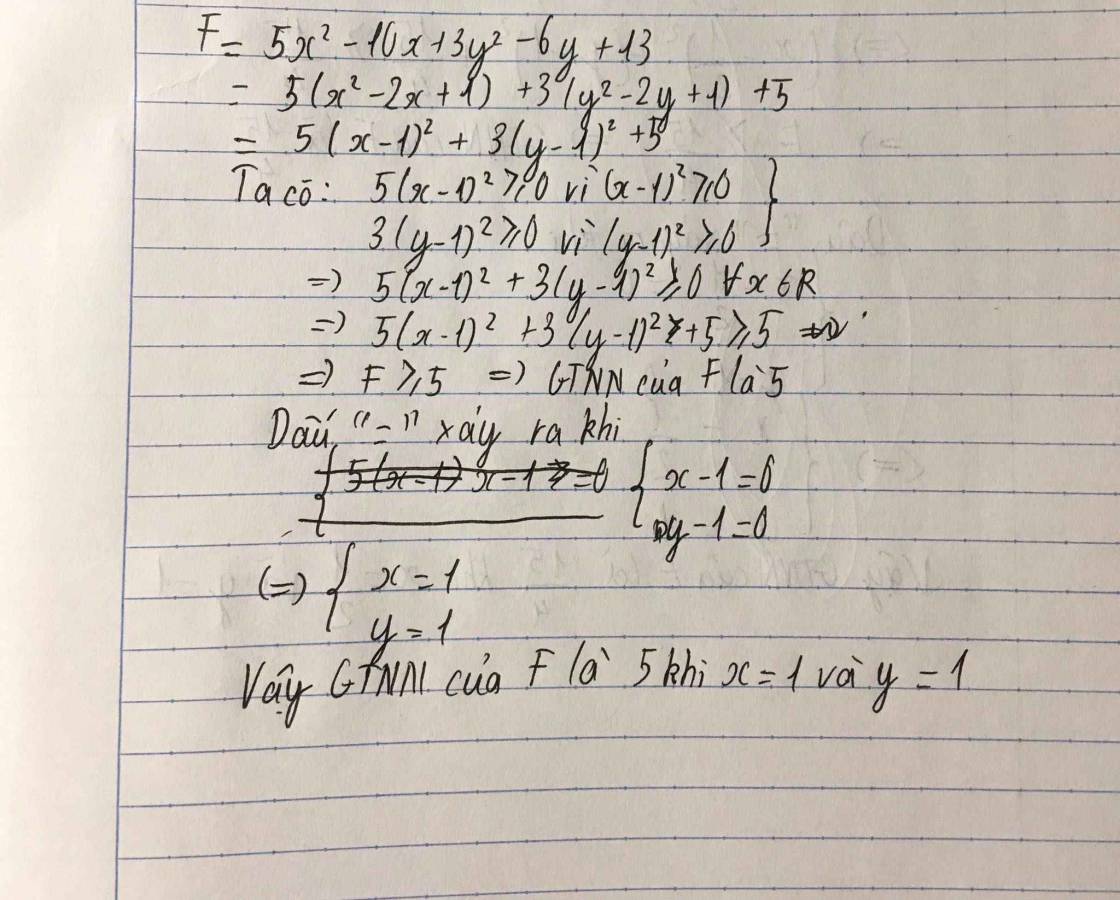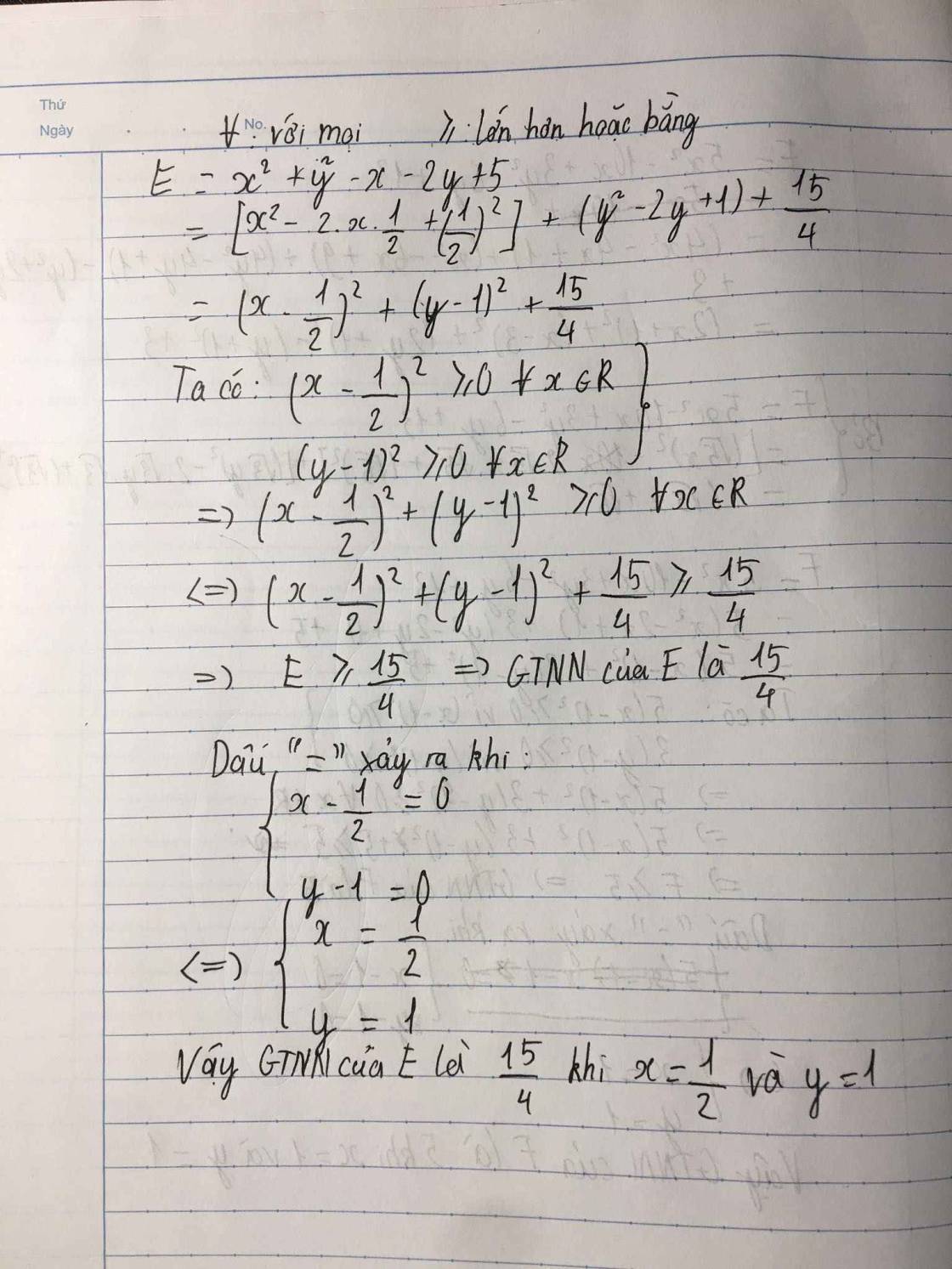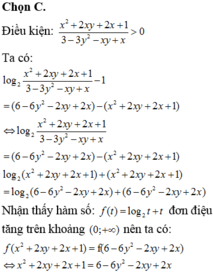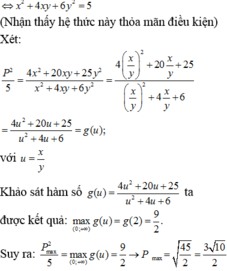Tìm GTNN của biểu thức M = x2 - 2x(y+1) + 3y2 + 2025

Những câu hỏi liên quan
1. cho x+y = 1 . tìm GTNN của biểu thức C = x2 + y2
2. cho x + 2y =1 . tìm GTNN của biểu thức P = x2 + 2y2
3. cho x + y =1 . tìm GTNN của biểu thức G = 2x2 + y2
4. cho x + y =1 . tìm GTNN của biểu thức H = x2 + 3y2
5. cho 2x + y =1 . tìm GTNN của biểu thức I = 4x2 + 2y2
6. tìm các số thực thõa mãn Pt :
2x2 + 5y2 + 8x - 10y + 13 = 0
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
Đúng 1
Bình luận (0)
tìm giá trị của biểu thức Q= 2x2-3xy/x2+3y2 với 2x+y=11z và 3x-y=4z
Ta có:
\(2x+y=11z\) và \(3x-y=4z\)
Chia theo vế ta có:
\(\dfrac{2x+y}{3x-y}=\dfrac{11z}{4z}=\dfrac{11}{4}\)
\(\Leftrightarrow4\left(2x+y\right)=11\left(3x-y\right)\)
\(\Leftrightarrow8x+4y=33x-11y\)
\(\Leftrightarrow15y=25x\)
\(\Leftrightarrow3y=5x\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{5}=k\)
\(\Rightarrow x=3k,y=5k\)
Thay vào Q ta có:
\(Q=\dfrac{2\cdot\left(3k\right)^2-3\cdot3k\cdot5k}{\left(3k\right)^2+3\cdot\left(5y\right)^2}\)
\(Q=\dfrac{18k^2-45k^2}{9k^2+75k^2}\)
\(Q=\dfrac{k^2\left(18-45\right)}{k^2\left(9+75\right)}\)
\(Q=\dfrac{-27}{84}=-\dfrac{9}{28}\)
Đúng 1
Bình luận (0)
\(\dfrac{2x+y}{3x-y}=\dfrac{11}{4}\)
=>33x-11y=8x+4y
=>25x=15y
=>5x=3y
=>x/3=y/5=k
=>x=3k; y=5k
\(Q=\dfrac{2\cdot9k^2-3\cdot3k\cdot5k}{9k^2+3\cdot25k^2}=\dfrac{18-9\cdot5}{9+3\cdot25}=\dfrac{-9}{28}\)
Đúng 1
Bình luận (0)
Cho các số x,y thỏa mãn đẳng thức 3x2+3y2+4xy- 2x+ 2y+203x2+3y2+4xy+2x−2y+20tính giá trị biểu thức M(x+y)2017+(x-2)2018+(y+ 1)20153x2+3y2+4xy+2x−2y+20tính giá trị biểu thứ(
Đọc tiếp
Cho các số x,y thỏa mãn đẳng thức
tính giá trị biểu thức M=(x+y)2017+(x-2)2018+(y+ 1)2015
3x^2+3y^2+4xy-2x+2y+2=0
=>2x^2+4xy+2y^2+x^2-2x+1+y^2+2y+1=0
=>x=1 và y=-1
M=(1-1)^2017+(1-2)^2018+(-1+1)^2015=1
Đúng 0
Bình luận (0)
tìm GTNN của biểu thức
E=x2+y2-x-2y+5
F=5x2-10x+3y2-6y+13
Bài 4: Cho x, y là hai số thỏa mãn : x + 2y = 3. Tìm giá trị nhỏ nhất của E = x2 + 2y2
Bài 5 : Cho hai số x, y thỏa mãn : x2 + 3y2 + 2xy – 10x – 14y + 18 = 0. Tìm GTLN ; GTNN của biểu thức P = x + y
bài 4 : ta có : \(x+2y=3\Leftrightarrow x=3-2y\)
\(\Rightarrow E=x^2+2y^2=\left(3-2y\right)^2+2y^2=4y^2-12y+9+2y^2\)
\(=6y^2-12y+6+3=6\left(y-1\right)^2+3\ge3\)
\(\Rightarrow E_{max}=3\) khi \(x=y=1\)
bài 5 : ta có : \(x^2+3y^2+2xy-10x-14y+18=0\)
\(\Leftrightarrow2y^2-4y+2=-\left(x^2+2xy+y^2\right)+10\left(x+y\right)-16\)
\(\Leftrightarrow2\left(y-1\right)^2=-\left(x+y\right)^2+10\left(x+y\right)-16\ge0\)
\(\Leftrightarrow2\le x+y\le8\)
\(\Rightarrow P_{min}=2\) khi \(\left\{{}\begin{matrix}y=1\\x+y=2\end{matrix}\right.\Leftrightarrow x=y=1\)
\(\Rightarrow P_{max}=8\) khi \(\left\{{}\begin{matrix}y=1\\x+y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=1\end{matrix}\right.\)
vậy ...........................................................................................................................
Đúng 0
Bình luận (0)
Tìm nghiệm của các đa thức sau
a)x2-2(x2-8) b)B(X)=3x-5-4(2x+3) c)M(y)=3y2-5y d) D(x)=2x2-3(x2+4)
Giúp tớ với bài khó quá ![]()
a: đặt \(x^2-2\left(x^2-8\right)=0\)
\(\Leftrightarrow16-x^2=0\)
=>x=4 hoặc x=-4
b: Đặt \(3x-5-4\left(2x+3\right)=0\)
=>3x-5-8x-12=0
=>-5x-17=0
=>-5x=17
hay x=-17/5
c: Đặt \(3y^2-5y=0\)
=>y(3y-5)=0
=>y=0 hoặc y=5/3
d: Đặt \(2x^2-3\left(x^2+4\right)=0\)
\(\Leftrightarrow-x^2-12=0\)
hay \(x\in\varnothing\)
Đúng 1
Bình luận (0)
Biết
x
2
+
y
2
1
. Tính giá trị của biểu thức
M
3
x
2
(
x
2
+
y
2
)
+
3
y
2
(...
Đọc tiếp
Biết x 2 + y 2 = 1 . Tính giá trị của biểu thức M = 3 x 2 ( x 2 + y 2 ) + 3 y 2 ( x 2 + y 2 ) – 5 ( y 2 + x 2 )
A. -8
B. 2
C. 8
D. -2
Ta có
M = 3 x 2 ( x 2 + y 2 ) + 3 y 2 ( x 2 + y 2 ) – 5 ( y 2 + x 2 ) = ( x 2 + y 2 ) ( 3 x 2 + 3 y 2 – 5 ) = ( x 2 + y 2 ) [ 3 ( x 2 + y 2 ) – 5 ]
Mà x 2 + y 2 = 1 nên M = 1.(3.1 – 5) = -2. Vậy M = -2
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Cho hai số thực x, y dương thỏa mãn:
log
2
x
2
+
2
x
y
+
2
x
+
1
3
-
3
y
2...
Đọc tiếp
Cho hai số thực x, y dương thỏa mãn: log 2 x 2 + 2 x y + 2 x + 1 3 - 3 y 2 - x y + x = 6 - x 2 - 4 x y - 6 y 2 Giá trị lớn nhất của biểu thức P=2x+5y bằng
![]()
![]()
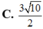
![]()
2) Cho x+ 3y = 1. Tìm GTNN của Q= x2 + 3y2