Rút gọn
A = \(16sin^2x.cos^2x.cos^22x+cos^24x\)
Những câu hỏi liên quan
Rút gọn biểu thức sau: A = \(\sqrt{sin^4x+sin^2x.cos^2x}\)
\(A=\sqrt{sin^2x\left(sin^2x+cos^2x\right)}=\sqrt{sin^2x}\)
=|sinx|
Đúng 2
Bình luận (0)
Thu gọn:
a/ cot^2x-cos^2x-cot^2x.cos^2x
b/ (sin^4x+cos^4x-1).(tan^2x+cot^2x+2)
Tìm giới hạn
B
lim
x
→
0
1
-
cos
x
.
cos
2
x
.
cos
3
x
x...
Đọc tiếp
Tìm giới hạn B = lim x → 0 1 - cos x . cos 2 x . cos 3 x x 2
A. +∞
B. -∞
C. 3
D. 0
Nghiệm của phương trình 8.cos 2x.xsin 2x.cos 4x= 2 là
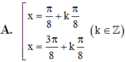
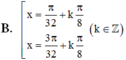
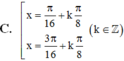
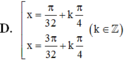
\(\cos^4x+\sin^2x.cos^2x+sin^2x\)
\(cos^4x+sin^2x.cos^2x+sin^2x\)
\(=cos^2x.cos^2x+sin^2x.cos^2x+sin^2x\)
\(=cos^2x\left(cos^2x+sin^2x\right)+sin^2x\)
\(=cos^2x.1+sin^2x\)
\(=cos^2x+sin^2x\)
\(=1\)
Đúng 0
Bình luận (0)
Cho \(0< x< 90^o\) . Chứng minh giá trị biểu thức sau không phụ thuộc vào giá trị của biến:
\(A=sin^6x+cos^6x+3sin^2x.cos^2x+tan^2x.cos^2x+cot^2x.sin^2x\)
Tính \(cos^4x+Sin^2x.cos^2x+\sin^2x\)
\(\left(sin^2x+cos^2x\right)cos^2x+sin^2x=cos^2x+sin^2x=1\)
Đúng 0
Bình luận (0)
a/ cot^2x-cos^2x-cot^2x.cos^2x
b/ (sin^4x+cos^4x-1).(tan^2x+cot^2x+2)
Giúp mình với ạ
c/m: sin^6x+cos^6x =1-3sin^2x.cos^2x = 1- 3/4sin^2 (2x)
= (sin^2x + cos^2x)^2 - 3sin^4x.cos^2x - 3sin^2x.cos^4x
= 1 - 3/4sin^2 (2x).sin^2x - 3/4sin^2(2x).cos^2x
= 1 - 3/4sin^2(2x)
Đúng 0
Bình luận (0)