Cho tam giác ABC vuông tại A có AB=4 và góc B=60° bán kính đường tròn nội tiếp của tam giác ABC là

Những câu hỏi liên quan
Cho tam giác ABC nhọn(AB<AC) có góc BAC = 60 độ nội tiếp trong đường tròn. Tiếp tuyến A của đường tròn cắt tia CB tại M. bán kính 0D vuông góc với BC tại E. Gọi N là giao điểm của AD và MC. Chứng minh tam giác AMN cân
ta có OD vuông góc với BC nên D là điểm chính giữa cung BC nên AD là phân giác góc BAC
nên góc BAD=góc CAD=60/2=30 độ hay góc BAN=30 độ
góc BAM=góc BCA( góc tạo bởi tiếp tuyến và dây và góc nội tiếp cùng chắn cung BA)
suy ra góc NAM=30 + góc BAM=30 độ+ góc BCA
mà góc ANM là góc ngoài tam giác NAC nên góc ANM= góc NAM+góc NCA=30 độ + góc BCA= gócNAM suy ra tam giác ANM cân ởM
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB<AC và BC =(\(4+4\sqrt{3}\) )cm. Tính số đo của góc B và C biết bán kính đường tròn nội tiếp tam giác ABC là 2cm
Cho tam giác ABC có AB=6cm AC=8cm BC=10cm
a) cm tam giác ABC vuông tại A
b) Tính góc B góc C và đường cao AH của tam giác ABC
c) Tính bán kính r của đường tròn (O) nội tiếp tam giác ABC
Cho tam giác $ABC$ vuông tại $A$. Đường tròn $(O)$ nội tiếp tam giác $ABC$ tiếp xúc với $AB$, $AC$ lần lượt tại $D$ và $E$.
a) Tứ giác $ADOE$ là hình gì?
b) Chứng minh \(S=p.r\) ($p$ là nửa chu vi tam giác $ABC$, $r$ là bán kính đường tròn nội tiếp).
b) Tính bán kính của đường tròn $(O)$ biết $AB = 6cm$, $AC = 8cm$.
BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr ( là chu vi của tam giác , là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).
giải:
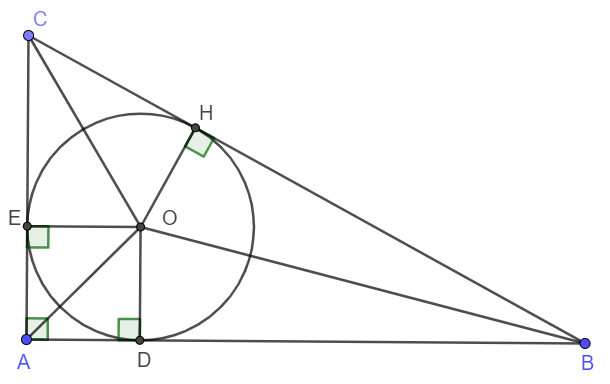
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có
( là chu vi của tam giác , là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: .
Diện tích tam giác ABC là: .
Chu vi tam giác ABC là: .
Suy ra: .
Xem thêm câu trả lời
cho tam giác ABC vuông tại A . I là tâm đường tròn nội tiếp tam giác có IH vuông góc với BC biết BH=5; CH=12. bán kính đường tròn nội tiếp bằng 6, một cạnh góc vuông =20. tính các cạnh của tam giác ABC
cho tam giác ABC vuông tại A . I là tâm đường tròn nội tiếp tam giác có IH vuông góc với BC biết BH=5; CH=12. bán kính đường tròn nội tiếp bằng 6, một cạnh góc vuông =20. tính các cạnh của tam giác ABC
Cho tam giác ABC vuông tại A. Gọi R là bán kính của đường tròn ngoại tiếp. r là bán kính của đường tròn nội tiếp tam giác ABC. Chứng minh rằng: AB + AC = 2(R + r)

Vì tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC.
Ta có: BC = 2R
Giả sử đường tròn (O) tiếp với AB tại D, AC tại E và BC tại F
Theo kết quả câu a) bài 58, ta có ADOE là hình vuông.
Suy ra: AD = AE = EO = OD = r
Theo tính chất hai tiếp tuyến cắt nhau ta có:
AD = AE
BD = BF
CE = CF
Ta có: 2R + 2r = BF + FC + AD + AE
= (BD + AD) + (AE + CE)
= AB + AC
Vậy AB = AC = 2(R + r)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R = 3cm. Tính diện tích hình quạt tạo bởi hai bán kính OB,OC và cung nhỏ BC khi \(\widehat{BAC}=60^o\)
2. Cho tam giác ABC vuông tại A có AB=6cm, AC=8cm nội tiếp đường tròn (O). Tính diện tích hình tròn (O)
2: ΔABC vuông tại A nội tiếp (O)
=>O là trung điểm của BC
BC=căn 6^2+8^2=10cm
=>OB=OC=10/2=5cm
S=5^2*3,14=78,5cm2
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ trục tọa độ Descarter vuông góc Oxy, cho tam giác ABC vuông tại A với B(-3;0) và C(7;0) , bán kính đường tròn nội tiếp tam giác là r= 2√10 -5. Tìm tọa độ tâm I của đường tròn nội tiếp tam giác ABC, biết I có tung độ dương.




















