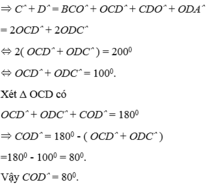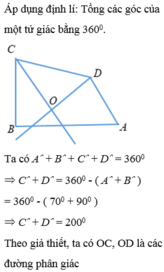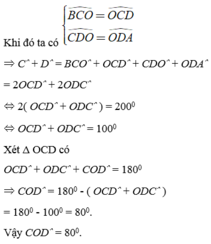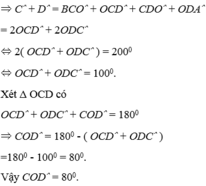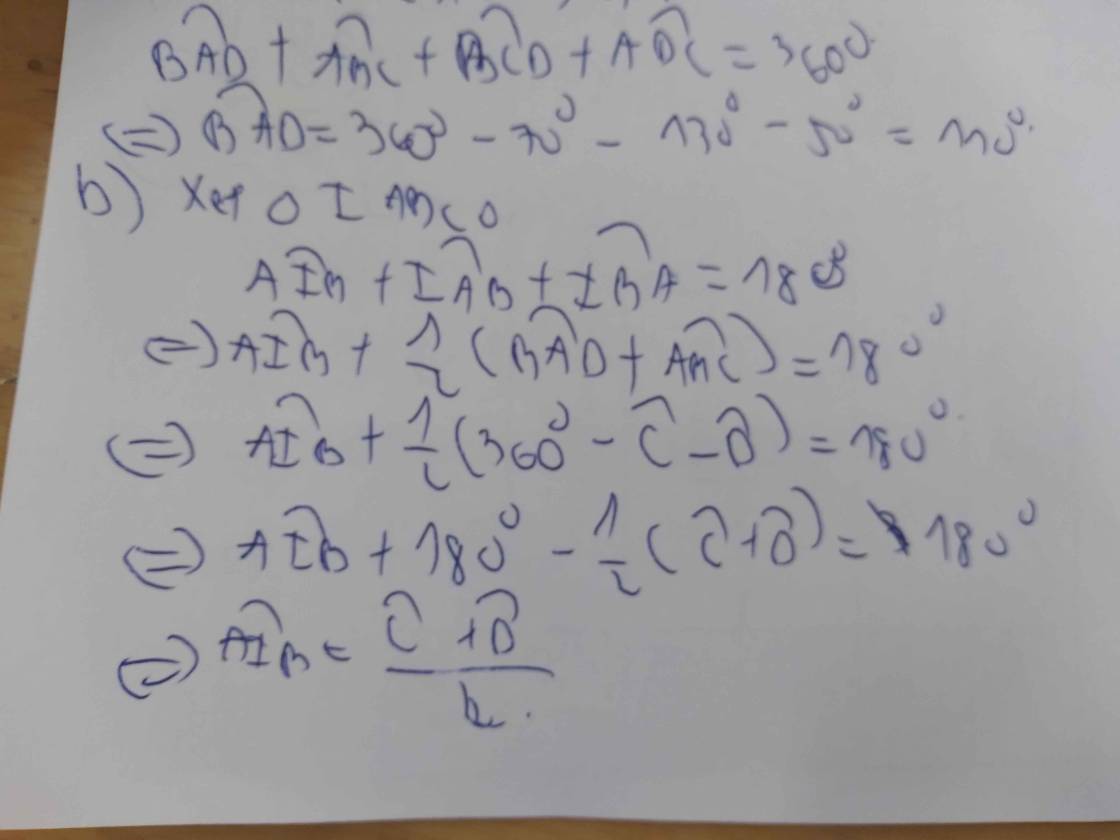Tứ giác ABCD có C=700,D=800,A-B=200.Tính số đo các góc A và B

Những câu hỏi liên quan
Tứ giác ABCD có Cˆ = 500, Dˆ = 800 , Aˆ - Bˆ = 200 . Tính số đo các góc A và B
Vì tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\\ \Leftrightarrow\left(\widehat{A}+\widehat{B}\right)+50^o+80^o=360^o\\ \Leftrightarrow\widehat{A}+\widehat{B}=230^o\)
Mặt khác: \(\widehat{A}-\widehat{B}=20^o\Rightarrow\widehat{A}=20^o+\widehat{B}\)
\(\Rightarrow\widehat{B}+20^o+\widehat{B}=230^o\\ \Leftrightarrow2\widehat{B}+20^o=230^o\\ \Leftrightarrow2\widehat{B}=210^o\\ \Leftrightarrow\widehat{B}=210^o:2=105^o\\ \Rightarrow\widehat{A}=20^o+105^o=125^o\)
Đúng 3
Bình luận (0)
Tổng 4 góc trong tứ giác là 360o
⇒ \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\)=360o
⇒ \(\widehat{A}+\widehat{B}+\)50o+80o=360o
⇒ \(\widehat{A}+\widehat{B}\)=230o
\(\widehat{A}+\widehat{B}\)=230o, \(\widehat{A}-\widehat{B}\)=20o⇒\(\widehat{A}+\widehat{B}+\widehat{A}-\widehat{B}\)=250o
⇒ \(2\widehat{A}\)=250o
⇒ \(\widehat{A}\)=125o
\(\widehat{A}+\widehat{B}\)=230o
⇒ 125o+\(\widehat{B}\)=230o
⇒\(\widehat{B}\)=105o
Đúng 2
Bình luận (0)
Tứ giác ABCD có A =700 ; B =800 ; C =900 . Số đo góc D là:
A. 1000 B. 1100 C. 1200 D. 1300
Cho tứ giác ABCD có A ^ = 70 0 , B ^ = 90 0 . Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc C O D ^ ?
Cho tứ giác ABCD có A ^ = 70 0 , B ^ = 90 0 . Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc C O D ^ ?
Cho tứ giác ABCD có A ^ = 70 0 , B ^ = 90 0 . Các tia phân giác của các góc C và D cắt nhau tại O. Tính số đo góc C O D ^ ?
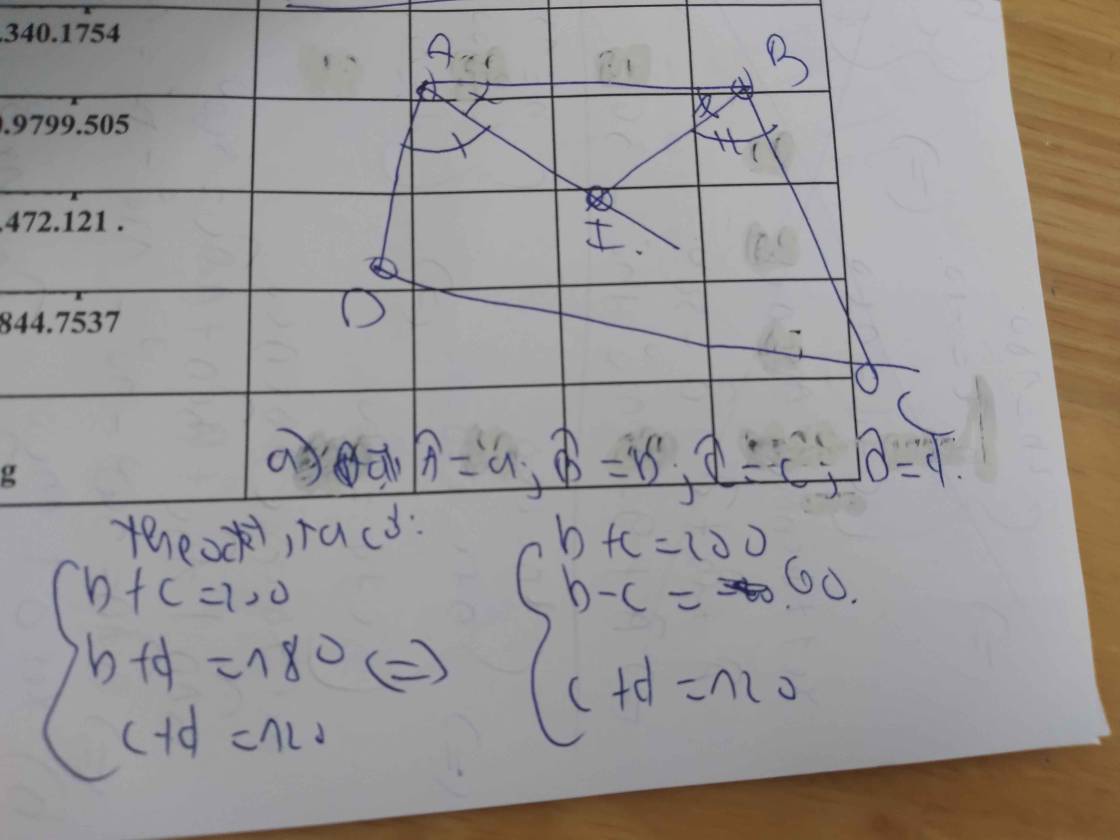
Cho tứ giác ABCD có B+C = 200°;B + D = 180°;C + D=120°.
a) Tính số đo các góc của tứ giác ABCD.
b) Gọi I là giao điểm của các tia phân giác của các góc BAD và ABC của tứ giác. Chứng minh AIB = C+D/2
Cho tam giác ABC vuông tại A có BC bằng 26cm và có độ dài các cạnh góc vuông tỉ lệ với 5 và 12.Tính độ dài các cạnh góc vuông AB và AC?
Cho tứ giác ABCD có A=700,B=1000,các tia phân giác của góc C và D cắt nhau tại O.Tính số đo COD
giúp mình với mình đang cần gấp ạ
a: Đặt \(\dfrac{AB}{5}=\dfrac{AC}{12}=k\)
=>AB=5k; AC=12k
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(25k^2+144k^2=26^2\)
=>\(k^2=4\)
=>k=2
=>AB=10cm; AC=24cm
b: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(\widehat{BCD}+\widehat{ADC}=360^0-70^0=290^0\)
=>\(2\cdot\left(\widehat{ODC}+\widehat{OCD}\right)=290^0\)
=>\(\widehat{OCD}+\widehat{ODC}=145^0\)
Xét ΔOCD có \(\widehat{COD}+\widehat{OCD}+\widehat{ODC}=180^0\)
=>\(\widehat{COD}=180^0-145^0=35^0\)
Đúng 1
Bình luận (0)
b1. Tứ giác ABCD có góc C= 60*, góc D = 80*; góc A - góc B = 10*. Tính số đo góc A và B.
b2. tứ giác ABCD có góc A = 110*; góc B = 100*. Các tia phân giác của góc C và D cắt nhau ở E. Các đường phân giác của các góc ngoài tại các đỉnh C và D cắt nhau ở F. Tính CED và CFD?
Bài 1 : Bài giải
Ta có : \(\widehat{A}-\widehat{B}=10^o\text{ }\Rightarrow\text{ }\widehat{A}=\widehat{B}+10^o\)
Trong tứ giác ABCD có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{B}+10+\widehat{B}+60^o+80^o=360^o\)
\(2\widehat{B}+150^o=360^o\)
\(2\widehat{B}=110^o\)
\(\widehat{B}=55^o\text{ }\Rightarrow\text{ }\widehat{A}=65^o\)
Tứ giác ABCD có ∠ C = 60 ° , ∠ D = 80 ° , ∠ A - ∠ B = 10 ° . Tính số đo các góc A và B.
Tổng bốn góc của 1 tứ giác bằng 360 ° nên: ∠A + ∠ B + ∠ C + ∠ D = 360 °
Suy ra: ∠ A + ∠ B = 360 ° – ( ∠ C + ∠ D) hay
∠ A + ∠ B = 360 ° - 60 ° + 80 ° = 220 °
Mà ∠ A - ∠ B = 10 °
Vậy
∠
A = 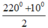 =
115
°
,
∠
B =
115
°
-
10
°
=
105
°
=
115
°
,
∠
B =
115
°
-
10
°
=
105
°
Đúng 0
Bình luận (0)