Hãy đo các góc dưới đây và so sánh số đo của chúng với 90°.
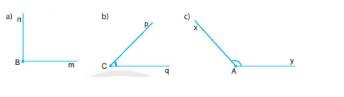
Bằng cách đo, hãy so sánh số đo các góc trong hình sau với \(90^\circ \).
\(\widehat{aOb} = 50^0 <90^0\)
\(\widehat{pMq} = 90^0\)
\(\widehat{mAn} = 110^0 >90^0\)
Bằng dụng cụ, hãy so sánh số đo của góc nội tiếp ∠(BAC) với số đo của cung bị chắn BC trong mỗi hình 16, 17, 18 dưới đây.
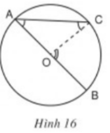

Sử dụng thước đo độ để đo các góc, từ đó ta rút ra kết luận:
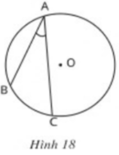
Bằng dụng cụ, hãy so sánh số đo của góc nội tiếp ∠(BAC) với số đo của cung bị chắn BC trong mỗi hình 16, 17, 18 dưới đây.
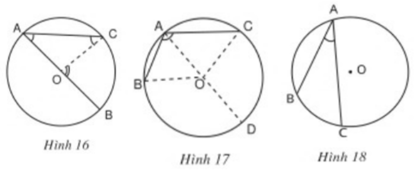
Sử dụng thước đo độ để đo các góc, từ đó ta rút ra kết luận:
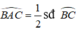
Trong hình vẽ dưới đây, hãy kể tên tất cả các góc. Dùng thước đo và sắp xếp số đo của chúng theo thứ tự giảm dần.
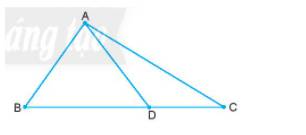
Các góc có trong hình là: \(\widehat {ABC},{\rm{ }}\widehat {BAC},{\rm{ }}\widehat {ACB},{\rm{ }}\widehat {BAD},{\rm{ }}\widehat {DAC},{\rm{ }}\widehat {BDA},{\rm{ }}\widehat {CDA},\widehat {CDB}\)
Đo các góc, ta được: \(\widehat {CDB} = 180^0, \widehat {CDA} = 127^0,\widehat {BDA}=94^0, \widehat {BAD}=72^0, \widehat {BDA}=55^0, \widehat {ACB}=31^0, \widehat {DAC}=22^0\)
Sắp xếp các góc theo thứ tự giảm dần, ta có: \(\widehat {CDB}, \widehat {CDA},{\rm{ }}\widehat {BDA},{\rm{ }}\widehat {BAD},{\rm{ }}\widehat {BDA},{\rm{ }}\widehat {ACB},{\rm{ }}\widehat {DAC}\)
a. Em hãy vẽ một tam giác tùy ý rồi dùng thước đo góc để đo các góc của tam giác đó.
b. Tính tổng các số đo của ba góc và so sánh với kết quả của bạn khác.
Chú ý: Nếu vẽ tam giác quá nhỏ thì sẽ khó đo góc.
a.
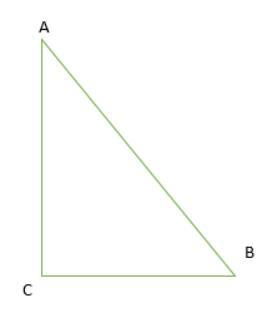
Góc CAB có số đo là 40 độ
Góc ABC có số đo là 50 độ
Góc ACB có số đo là 90 độ
b. Tổng ba góc trong tam giác là: 180 độ bằng với kết quả của các bạn khác.
Quan sát Hình 10.
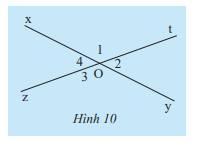
a) Hãy dùng thước đo góc để đo \(\widehat {{O_1}}\)và \(\widehat {{O_3}}\). So sánh số đo hai góc đó.
b) Hãy dùng thước đo góc để đo \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\). So sánh số đo hai góc đó.
Ta có:
\(\begin{array}{l}a)\widehat {{O_1}} = 135^\circ ;\widehat {{O_3}} = 135^\circ \Rightarrow \widehat {{O_1}} = \widehat {{O_3}}\\b)\widehat {{O_2}} = 45^\circ ;\widehat {{O_4}} = 45^\circ \Rightarrow \widehat {{O_2}} = \widehat {{O_4}}\end{array}\)
1So sánh các cạnh của ∆ABC biết rằng: Số đo cácA,B,C lần lượt tỉ lệ với 2,3,4 .
2. So sánh các cạnh của ∆ABC biết rằng: A=110 độ và số đo góc B, C lỉ lệ với 1/3 và 1/4.
3.So sánh các cạnh của ∆ABC biết rằng: A=40 độ và số đo góc B, C tỉ lệ với 3,4.
4.Cho ∆ABCcó AB=5cm,BC=7cm,AC=10cm . So sánh các góc của ∆ABC ?
1:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}=\dfrac{a+b+c}{2+3+4}=\dfrac{180}{9}=20\)
Do đó: a=40; b=60; c=80
Xét ΔABC có \(\widehat{A}< \widehat{B}< \widehat{C}\)
nen BC<AC<AB
2: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{b}{\dfrac{1}{3}}=\dfrac{c}{\dfrac{1}{4}}=\dfrac{b+c}{\dfrac{1}{3}+\dfrac{1}{4}}=\dfrac{70}{\dfrac{7}{12}}=120\)
Do đó: b=40; c=30
Xét ΔABC có \(\widehat{A}>\widehat{B}>\widehat{C}\)
nên BC>AC>AB
Lúc 6h15 số đo của góc được tạo bởi kim giờ và kim phút. So sánh góc của đồng hồ với 90 độ