Vẽ các parabol sau:
a) \({y^2} = 16x\)
b) \({y^2} = x\)
c) \({y^2} = 32x\)
Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:
a) \({y^2} = 12x\)
b) \({y^2} = x\)
a) Từ phương trình chính tắc \({y^2} = 12x\) ta có \(p = 6\)
Suy ra
+) Tiêu điểm của parabol \(F(3;0)\)
+) Phương trình đường chuẩn của parabol \(\Delta :x + 3 = 0\)
b) Từ phương trình chính tắc \({y^2} = x\) ta có \(p = \frac{1}{2}\)
Suy ra
+) Tiêu điểm của parabol \(F(\frac{1}{4};0)\)
+) Phương trình đường chuẩn của parabol \(\Delta :x + \frac{1}{4} = 0\)
Rút gọn các phân thức sau:
a) \(\dfrac{6x^2y^2}{8xy^{ }5}\)
b) \(\dfrac{10xy^2\left(x+y\right)}{15xy\left(x+y\right)^3}\)
c) \(\dfrac{2x^2+2x
}{x+1}\)
d) \(\dfrac{x^2-xy-x+y}{x^2+xy-x-y}\)
e) \(\dfrac{36\left(x-2\right)^3}{32-16x}\)
a) \(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x}{4y^3}\)
b) \(=\dfrac{2y}{3\left(x+y\right)^2}=\dfrac{2y}{3x^2+6xy+3y^2}\)
c) \(=\dfrac{2x\left(x+1\right)}{x+1}=2x\)
d) \(=\dfrac{x\left(x-y\right)-\left(x-y\right)}{x\left(x+y\right)-\left(x+y\right)}=\dfrac{\left(x-y\right)\left(x-1\right)}{\left(x+y\right)\left(x-1\right)}=\dfrac{x-y}{x+y}\)
e) \(=\dfrac{36\left(x-2\right)^3}{-16\left(x-2\right)}=-9\left(x-2\right)^2=-9x^2+36x-36\)
Vẽ đồ thị các hàm số sau:
a) \(y = 2{x^2} + 4x - 1\)
b) \(y = - {x^2} + 2x + 3\)
c) \(y = - 3{x^2} + 6x\)
d) \(y = 2{x^2} - 5\)
Tham khảo:
a)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} + 4x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 4}}{{2.2}} = - 1;{y_S} = 2.{( - 1)^2} + 4.( - 1) - 1 = - 3.\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua điểm có tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
b)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 2}}{{2.( - 1)}} = 1;{y_S} = - {1^2} + 2.1 + 3 = 4.\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.

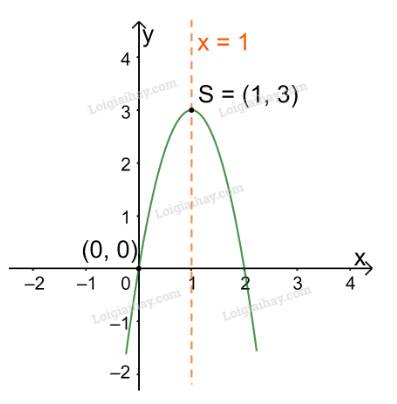
c)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - 3{x^2} + 6x\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 6}}{{2.( - 3)}} = 1;{y_S} = - {3.1^2} + 6.1 = 3\)
+ Có trục đối xứng là đường thẳng \(x = 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 3 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 0, tức là đồ thị đi qua gốc tọa độ (0; 0).
Ta vẽ được đồ thị như hình dưới.
d)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = 2{x^2} - 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.2}} = 0;{y_S} = {2.0^2} - 5 = - 5.\)
+ Có trục đối xứng là đường thẳng \(x = 0\) (trùng với trục Oy);
+ Bề lõm quay lên trên vì \(a = 2 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng -5, tức là đồ thị đi qua điểm có tọa độ (0; -5).
Ta vẽ được đồ thị như hình dưới.

Vẽ đồ thị các hàm số sau:
a) \(y = {x^2} - 4x + 3\)
b) \(y = - {x^2} - 4x + 5\)
c) \(y = {x^2} - 4x + 5\)
d) \(y = - {x^2} - 2x - 1\)
Tham khảo:
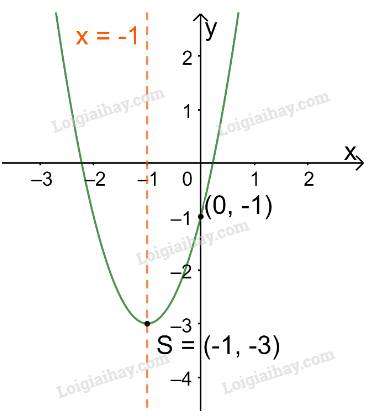
a)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 3\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
b)
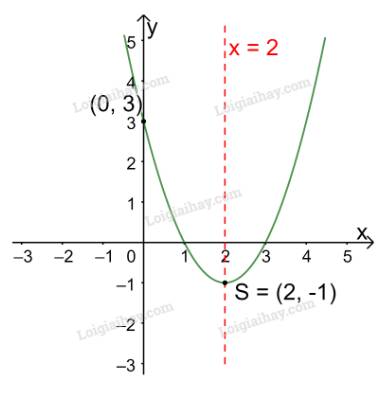
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.( - 1)}} = - 2;{y_S} = - {( - 2)^2} - 4.( - 2) + 5 = 9.\)
+ Có trục đối xứng là đường thẳng \(x = - 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
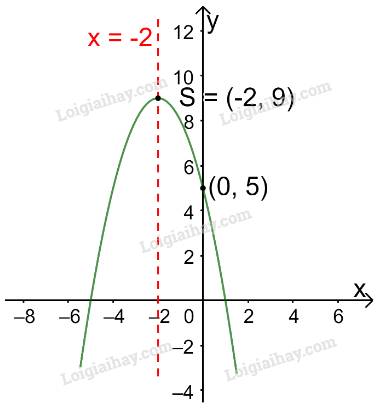
c) Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = {x^2} - 4x + 5\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 5 = 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).
Ta vẽ được đồ thị như hình dưới.
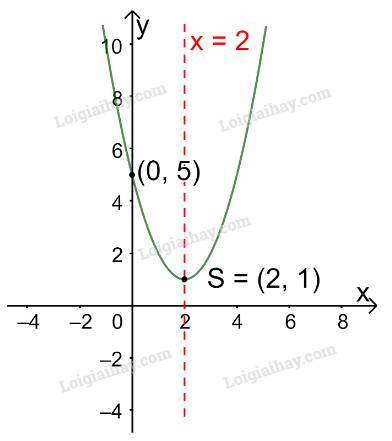
d)
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = - {x^2} - 2x - 1\) là một parabol (P):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 2)}}{{2.( - 1)}} = - 1;{y_S} = - {( - 1)^2} - 2.( - 1) - 1 = 0\)
+ Có trục đối xứng là đường thẳng \(x = - 1\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay xuống dưới vì \(a = - 1 < 0\)
+ Cắt trục tung tại điểm có tung độ bằng -1, tức là đồ thị đi qua gốc tọa độ (0; -1).
Ta vẽ được đồ thị như hình dưới.
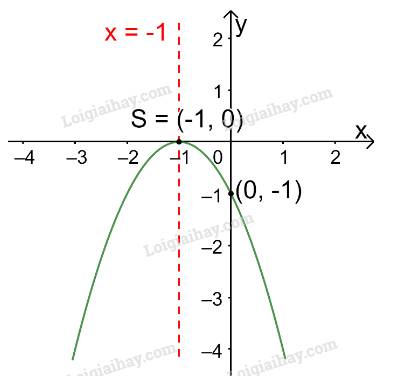
Vẽ đồ thị các hàm số bậc hai sau:
a) \(y = - {x^2} + 4x - 3\)
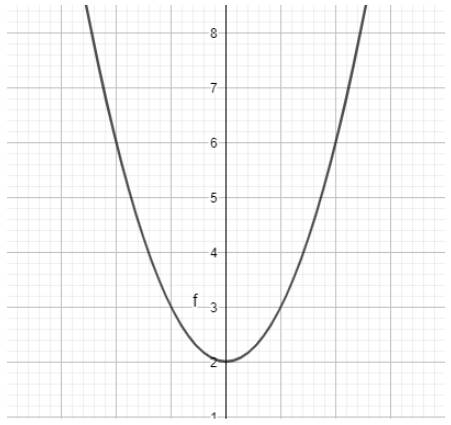
b) \(y = {x^2} + 2\)
c) \(y = \frac{1}{2}{x^2} + x + 1\)
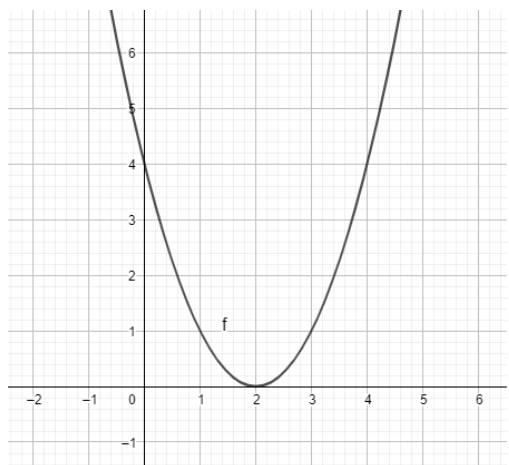
d) \(y = {x^2} - 4x + 4\)
a)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=-x^2+4x-3 vào vùng nhập lệnh như hình bên
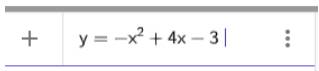
Ta có ngay parabol trên vùng làm việc như hình dưới:
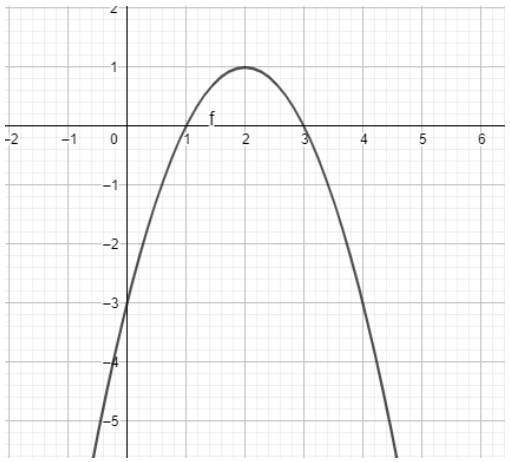
b)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2+2 vào vùng nhập lệnh như hình bên
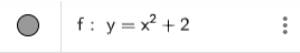
Ta có ngay parabol trên vùng làm việc như hình dưới:
c)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=1/2x^2+x+1 vào vùng nhập lệnh như hình bên
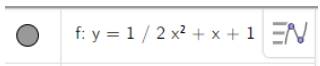
Ta có ngay parabol trên vùng làm việc như hình dưới:
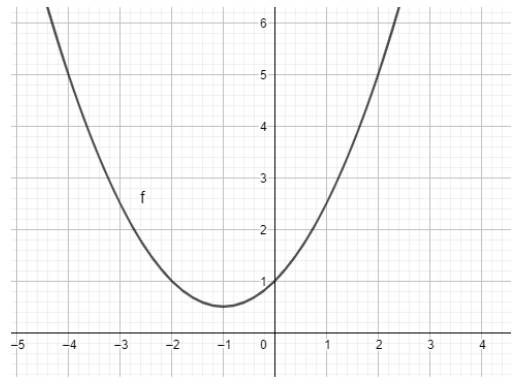
d)
1. Khởi động phần mềm đã cài đặt hoặc truy cập vào trang web: https://www.geogebra.org để sử dụng phiên bản online
2. Nhập phương trình bậc hai theo cú pháp y=x^2-4x+4 vào vùng nhập lệnh như hình bên
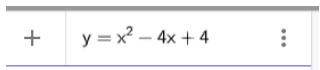
Ta có ngay parabol trên vùng làm việc như hình dưới:
Vẽ hình trong mỗi trường hợp sau:
a) Vẽ hypebol biết hai tiêu điểm \({F_1}( - 5;0),{F_2}(5;0)\) và điểm \((3;0)\) thuộc hypebol;
b) Vẽ parabol biết phương trình chính tắc: \({y^2} = 5x\);
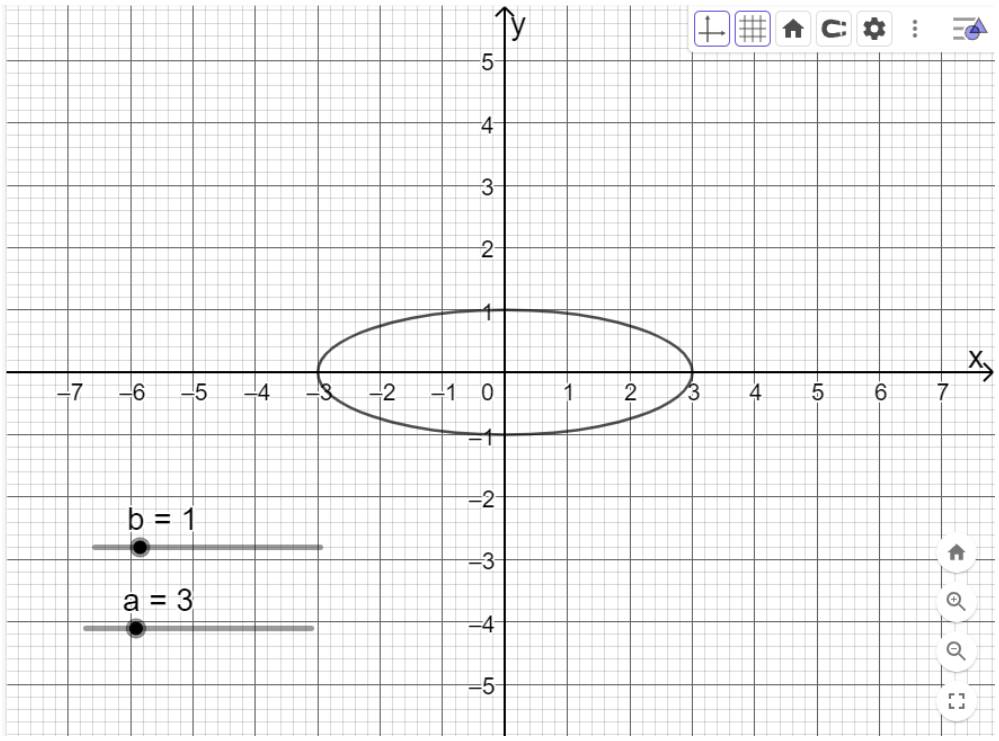
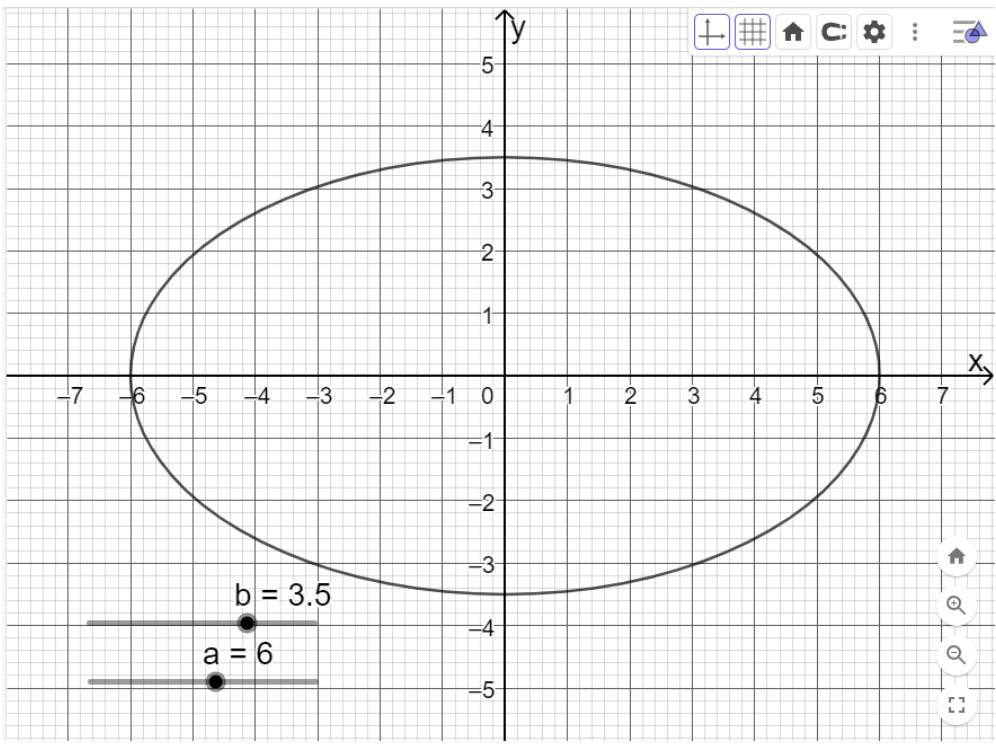
c) Vẽ elip tại các giá trị \(a = 3,b = 1\) và \(a = 6,b = 3,5.\)
a) Nhập lệnh: Hypebon((-5,0),(5,0),(3,0)) vào ô nhập lệnh rồi bấm enter.
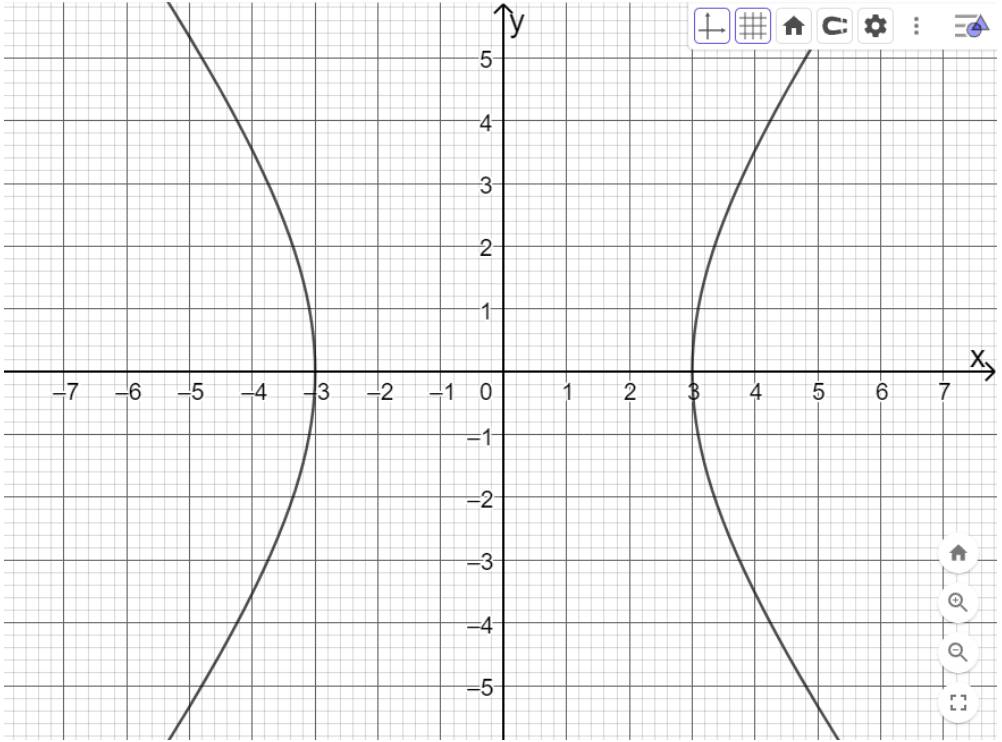
b) Nhập lệnh: y^2=5*x vào ô nhập lệnh rồi bấm enter
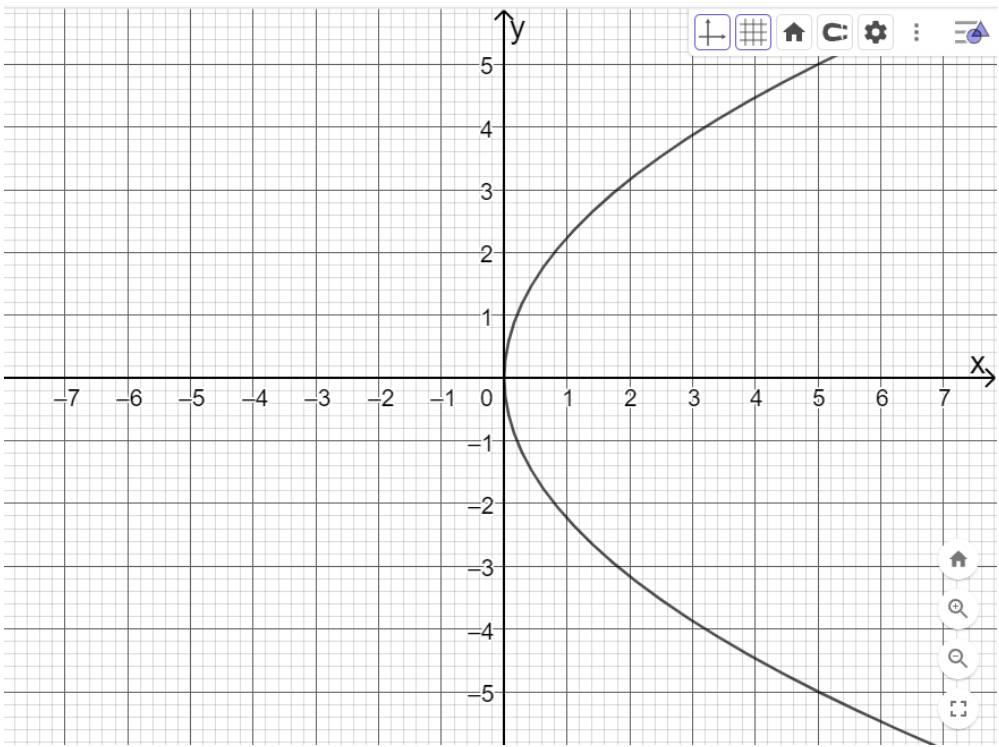
c)
Bước 1: Tạo thanh trượt a: Nháy vào biểu tượng thanh trượt, sau đó nháy cuột lên vùng làm việc, khi đó trên vùng làm việc xuất hiện bảng cho phép thiết lập thông tinh cho thanh trượt: Tên thanh trượt (a), giá trị dạng số/ số nguyên, giá trị cực tiểu (1), giá trị cực đại (10).
Bước 2: Tạo thanh trượt b: Làm tương tự với thiết lập thông tin chẳng hạn như:
Tên thanh trượt (b), giá trị dạng số, giá trị cực tiểu (0), giá trị cực đại (5), số gia (0,5).
Bước 3: Nhập phương trình chính tắc của elip vào ô Nhập lệnh:
x^2 / a^2 + y^2 / b^2 =1 và bấm enter.
Di chuyển trên thanh trượt vào giá trị a=3, b=1 ta được như hình dưới
Di chuyển trên thanh trượt vào giá trị a=6, b=3,5 ta được như hình dưới
1 vẽ đồ thị hàm số y= x²/2 (P) 2 bằng phép tính hãy xác định toạ độ các giáo điểm parabol (P) với đưownhf thẳng (d) có phương trình y=-1/2 x+1 3 với các giá trị nào của m thì đường thẳng (d) y=X+m a cắt parabol (P) b tiếp xúc với parabol c không cắt parabol
Vẽ các hypebol sau:
a) \(\frac{{{x^2}}}{{10}} - \frac{{{y^2}}}{6} = 1\)
b) \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 - y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:

b) Nhập phương trình hypebol theo cú pháp x^2/4 - y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
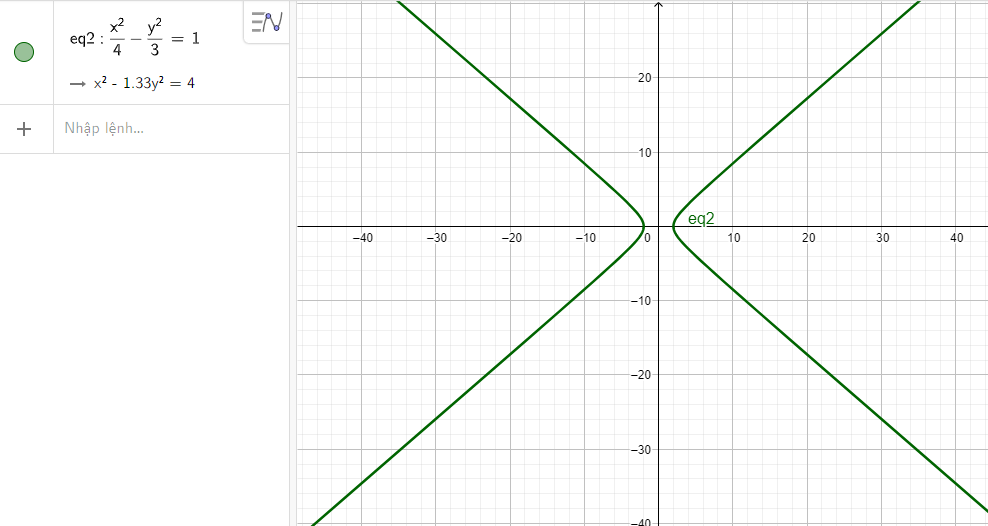
c) Nhập phương trình hypebol theo cú pháp x^2/64 - y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:

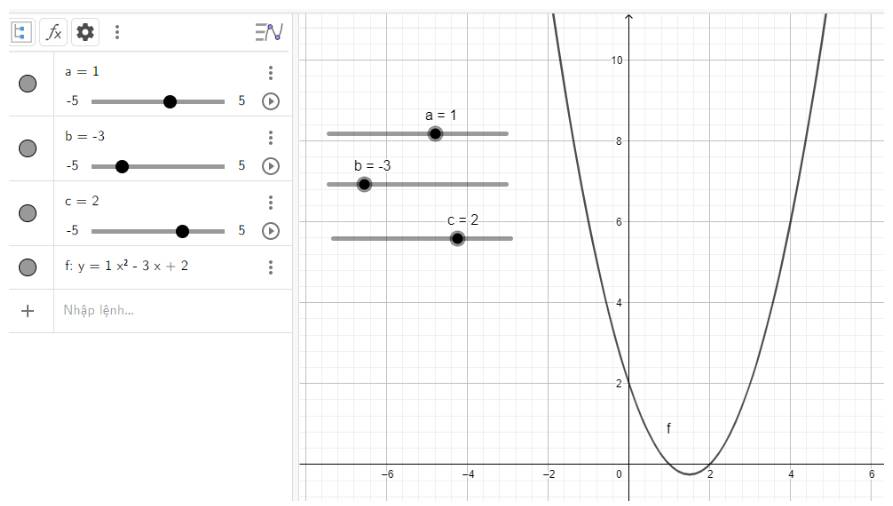
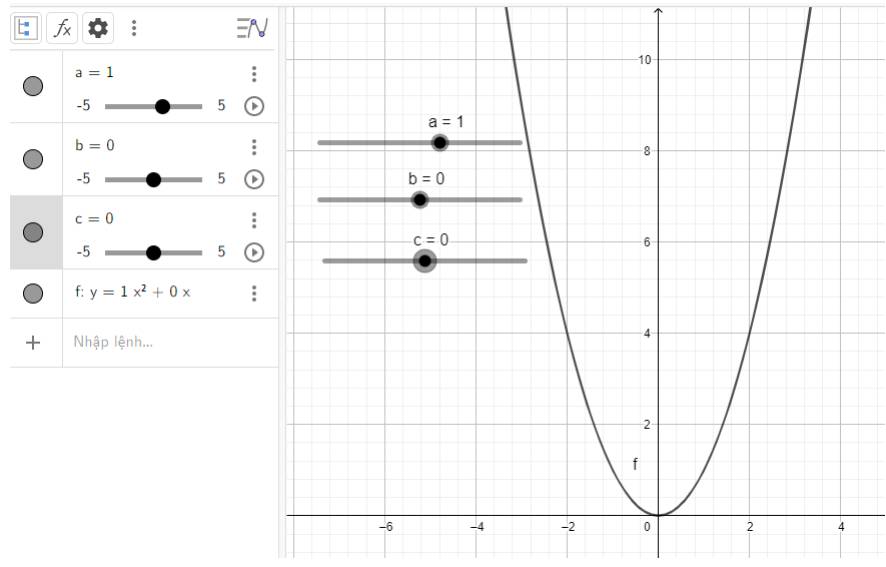
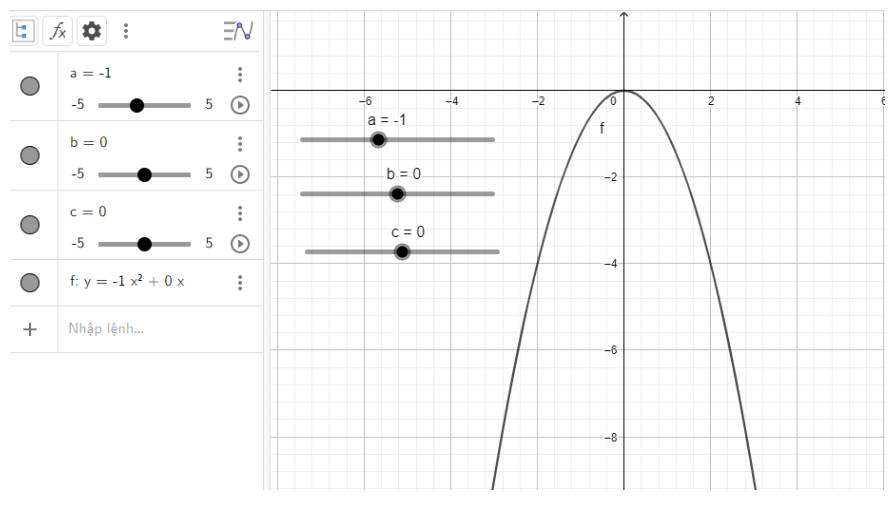
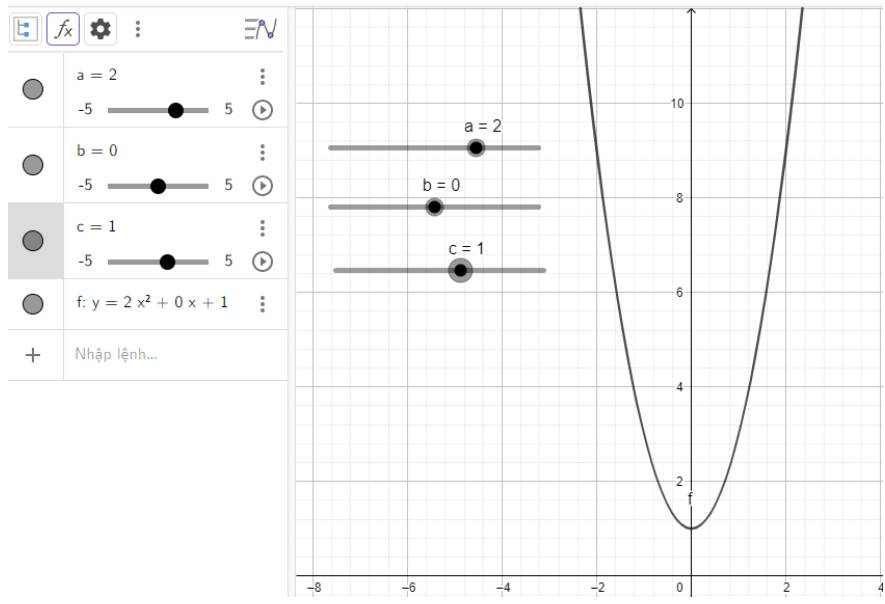
Điều chỉnh a, b, c để vẽ được nhiều dạng parabol khác nhau:
a) \(\)\(y = {x^2} - 3x + 2\)
b) \(y = {x^2}\)
c) \(y = - {x^2}\)
d) \(y = 2{x^2} + 1\)
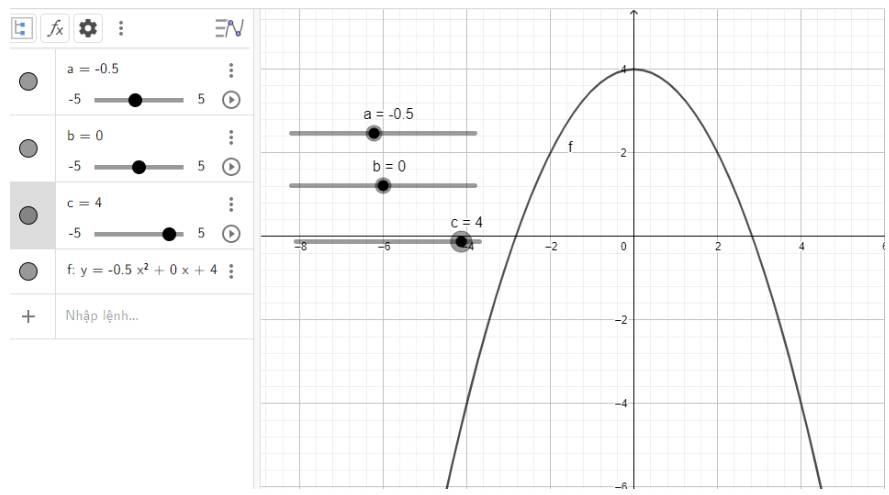
e) \(y = - \frac{1}{2}{x^2} + 4\)
Thực hiện các bước đã nêu ở phương pháp ta có các hình dưới đây
a) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung và trục hoành lần lượt tại điểm có tọa độ là (0; 2) và (2; 0)
b) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
c) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, đi qua gốc tọa độ và đỉnh chính là gốc tọa độ
d) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía trên, cắt trục tung tại điểm có tung độ là 1 đó cũng chính là đỉnh của parabol
e) Quan sát vào đồ thị ta thấy:
Đồ thị quay bề lõm về phía dưới, cắt trục tung tại điểm có tung độ là 4 đó cũng chính là đỉnh của parabol