Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ \(\overrightarrow x \);
b) Cùng hướng với vectơ \(\overrightarrow a \) ;
Ngược hướng với vectơ \(\overrightarrow u \).
Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ \(\overrightarrow x \);
b) Cùng hướng với vectơ \(\overrightarrow a \) ;
Ngược hướng với vectơ \(\overrightarrow u \).
Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \)được gọi là cùng hướng, còn hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ \(\overrightarrow a \) và các vectơ ngược hướng với vectơ \(\overrightarrow a \).
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.
Cho hình thang ABCD có hai cạnh đáy là AB và DC (hình 15). Điểm M nằm trên đoạn DC.
a) Gọi tên các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \)
b) Gọi tên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)
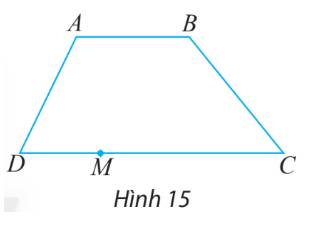
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC} \)
b) \(\overrightarrow {DM} \)có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD} \)
Cho hình bình hành ABCD tâm O. Gọi M và N lần lượt là trung điểm của AD và BC. Dựa vào các điểm A, B, C, D, O, M, N đã cho, hãy :
a) Kể tên hai vectơ cùng phương với \(\overrightarrow{AB}\), hai vectơ cùng hướng với \(\overrightarrow{AB}\), hai vectơ ngược hướng với \(\overrightarrow{AB}\) (các vectơ kể ra này đều khác \(\overrightarrow{0}\)
b) Chỉ ra một vectơ bằng vectơ \(\overrightarrow{MO}\) , một vectơ bằng vectơ \(\overrightarrow{OB}\) ?
a)
Các véc tơ cùng phương với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{OM};\overrightarrow{MN};\overrightarrow{NM};\overrightarrow{NO};\overrightarrow{ON};\overrightarrow{DC};\overrightarrow{CD};\overrightarrow{BA};\overrightarrow{AB}\).
Hai véc tơ cùng hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{ON}\).
Hai véc tơ ngược hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{OM};\overrightarrow{ON}\).
b) Một véc tơ bằng véc tơ \(\overrightarrow{MO}\) là: \(\overrightarrow{ON}\).
Một véc tơ bằng véc tơ \(\overrightarrow{OB}\) là: \(\overrightarrow{DO}\).
Gọi O là tâm hình lục giác đều ABCDEF.
a) Tìm các vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \).
b) Tìm các vectơ bằng vectơ \(\overrightarrow {AB} \).
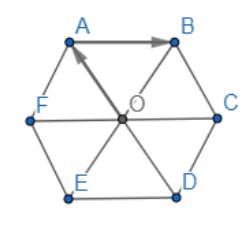
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \) là : \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF} \)
b) Ta có: \(OA = OB = OC = OD = OE = FO\) và AB // FC // ED
Suy ra các vectơ bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} \)
Quan sát Hình 39 và cho biết vị trí tương đối giữa giá của vectơ \(\overrightarrow {CD} \) với giá của vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {PQ} \).
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Giá của vectơ \(\overrightarrow {PQ} \) là đường thẳng PQ.
Dễ thấy: AB // CD và CD trùng PQ.
Quan sát hai biển báo ở Hình 40a, 40b, cho biết hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng hướng hay không.
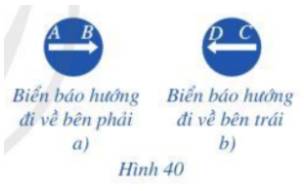
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: đường thẳng AB trùng với đường thẳng CD.
Do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng phương.
Lại có: vectơ \(\overrightarrow {AB} \) chỉ hướng đi về bên phải còn vectơ \(\overrightarrow {CD} \) chỉ hướng đi về bên trái.
Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có ngược hướng.
Quan sát hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) ở hình 42.
a) Nhận xét về phương của hai vectơ đó.
b) Nhận xét về hướng của hai vectơ đó.
c) So sánh độ dài của hai vectơ đó.
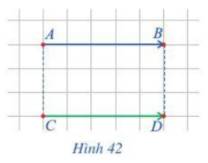
a) Ta có:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
b) Quan sát hình 42, ta thấy cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: \(|\overrightarrow {AB} |\; = AB\); \(|\overrightarrow {CD} |\; = CD\) và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.
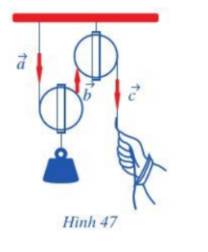
Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)(Hình 47).
a) Hãy chỉ ra các cặp vectơ cùng phương.
b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.

Gọi a, b, c là các đường thẳng lần lượt chứa các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \).
Khi đó: a, b, c lần lượt là giá của các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)
a) Dễ thấy: a // b // c
\( \Rightarrow \) Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) cùng phương với nhau.
Vậy các cặp vectơ cùng phương là: \(\overrightarrow a \) và \(\overrightarrow b \), \(\overrightarrow a \) và \(\overrightarrow c \), \(\overrightarrow b \) và \(\overrightarrow c \).
b) Quan sát ba vectơ, ta thấy: vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng hướng xuống còn vectơ \(\overrightarrow b \) hướng lên trên.
Vậy vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng hướng, vectơ \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng, vectơ \(\overrightarrow b \) và \(\overrightarrow c \) ngược hướng.