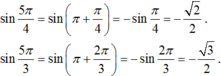Tính các giá trị lượng giác: \(\sin {120^o};\cos {150^o};\cot {135^o}.\)

Những câu hỏi liên quan
Cho biết \(\sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1.\) Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của \(E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.\)
Ta có:
\(\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o} = \frac{1}{2};\\\tan {135^o} = - \tan \left( {{{180}^o} - {{135}^o}} \right) = - \tan {45^o} = - 1\end{array}\)
\( \Rightarrow E = 2.\frac{{\sqrt 3 }}{2} + \frac{1}{2} - 1 = \sqrt 3 - \frac{1}{2}.\)
Đúng 0
Bình luận (0)
Tính giá trị của các biểu thức sau:
a) \(M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
b) \(N = \sin {60^o}.\cos {30^o} + \frac{1}{2}.\sin {45^o}.\cos {45^o}\)
c) \(P = 1 + {\tan ^2}{60^o}\)
d) \(Q = \frac{1}{{{{\sin }^2}{{120}^o}}} - {\cot ^2}{120^o}.\)
a) \(M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
Ta có: \(\left\{ \begin{array}{l}\sin {45^o} = \cos {45^o} = \frac{{\sqrt 2 }}{2};\;\\\sin {30^o} = \frac{1}{2}\end{array} \right.\)
Thay vào M, ta được: \(M = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} + \frac{1}{2} = \frac{2}{4} + \frac{1}{2} = 1\)
b) \(N = \sin {60^o}.\cos {30^o} + \frac{1}{2}.\sin {45^o}.\cos {45^o}\)
Ta có: \(\sin {60^o} = \frac{{\sqrt 3 }}{2};\;\;\cos {30^o} = \frac{{\sqrt 3 }}{2};\;\sin {45^o} = \frac{{\sqrt 2 }}{2};\, \cos {45^o}= \frac{{\sqrt 2 }}{2}\)
Thay vào N, ta được: \(N = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{1}{2}.\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} = \frac{3}{4} + \frac{1}{4} = 1\)
c) \(P = 1 + {\tan ^2}{60^o}\)
Ta có: \(\tan {60^o} = \sqrt 3 \)
Thay vào P, ta được: \(Q = 1 + {\left( {\sqrt 3 } \right)^2} = 4.\)
d) \(Q = \frac{1}{{{{\sin }^2}{{120}^o}}} - {\cot ^2}{120^o}.\)
Ta có: \(\sin {120^o} = \frac{{\sqrt 3 }}{2};\;\;\cot {120^o} = \frac{{ - 1}}{{\sqrt 3 }}\)
Thay vào P, ta được: \(Q = \frac{1}{{{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}} - \;{\left( {\frac{{ - 1}}{{\sqrt 3 }}} \right)^2} = \frac{1}{{\frac{3}{4}}} - \;\frac{1}{3} = \;\frac{4}{3} - \;\frac{1}{3} = 1.\)
Đúng 0
Bình luận (0)
Tính giá trị đúng của các biểu thức sau (không dùng máy tính cầm tay):
a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
b) \(B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}\)
c) \(C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {0^o} = 1;\;\cos {120^o} = - \frac{1}{2}\)
Lại có: \(\cos {140^o} = - \cos \left( {{{180}^o} - {{40}^o}} \right) = - \cos {40^o}\)
\(\begin{array}{l} \Rightarrow A = 1 + \cos {40^o} + \left( { - \frac{1}{2}} \right) - \cos {40^o}\\ \Leftrightarrow A = \frac{1}{2}.\end{array}\)
b) \(B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\;\sin {180^o} = 0\)
Lại có: \(\sin {175^o} = \sin \left( {{{180}^o} - {{175}^o}} \right) = \sin {5^o}\)
\(\begin{array}{l} \Rightarrow B = \sin {5^o} + \frac{1}{2} - \sin {5^o} + 0\\ \Leftrightarrow B = \frac{1}{2}.\end{array}\)
c) \(C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}\)
Ta có: \(\sin {75^o} = \cos\left( {{{90}^o} - {{75}^o}} \right) = \cos {15^o}\); \(\sin {55^o} = \cos\left( {{{90}^o} - {{55}^o}} \right) = \cos {35^o}\)
\(\begin{array}{l} \Rightarrow C = \cos {15^o} + \cos {35^o} - \cos {15^o} - \cos {35^o}\\ \Leftrightarrow C = 0.\end{array}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
Ta có: \(\tan {115^o} = - \tan \left( {{{180}^o} - {{115}^o}} \right) = - \tan {65^o}\)
Mà: \(\tan {65^o} = \cot \left( {{{90}^o} - {{65}^o}} \right) = \cot {25^o}\)
\(\begin{array}{l} \Rightarrow D = \tan {25^o}.\tan {45^o}.(-\cot {25^o})\\ \Leftrightarrow D =- \tan {45^o} = -1\end{array}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
Ta có: \(\cot {100^o} = - \cot \left( {{{180}^o} - {{100}^o}} \right) = - \cot {80^o}\)
Mà: \(\cot {80^o} = \tan \left( {{{90}^o} - {{80}^o}} \right) = \tan {10^o}\Rightarrow \cot {100^o} =- \tan {10^o}\)
\(\begin{array}{l} \Rightarrow E = \cot {10^o}.\cot {30^o}.(-\tan {10^o})\\ \Leftrightarrow E = -\cot {30^o} =- \sqrt 3 .\end{array}\)
Đúng 0
Bình luận (0)
Tính các giá trị lượng giác còn lại của góc
α
biết
sin
α
3
5
A.
cos
α
3
4
;
tan
α
3
4
;
c
o
t
α
4
5...
Đọc tiếp
Tính các giá trị lượng giác còn lại của góc α biết sin α = 3 5
A. cos α = 3 4 ; tan α = 3 4 ; c o t α = 4 5
B. cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 3
C. cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 5
B. cos α = 3 4 ; tan α = 4 5 ; c o t α = 4 3
Ta có sin α = 3 5 suy ra sin 2 α = 9 25 , mà sin 2 α + cos 2 α = 1 , do đó:
cos 2 α = 1 - sin 2 α = 1 - 9 25 = 16 25 suy ra cos α = 4 5
Do đó:
tan α = sin α cos α = 3 5 : 4 5 = 3 5 . 5 4 = 3 4
c o t α = cos α sin α = 4 5 : 3 5 = 4 5 . 5 3 = 4 3
Vậy cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 3
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Tìm các giá trị lượng giác của góc \({120^o}\) (H.3.4)
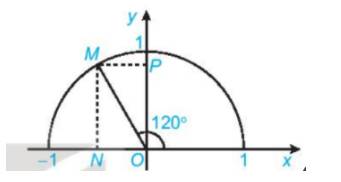
Tham khảo:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\)
Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Vì \(\widehat {xOM} = {120^o} > {90^o}\) nên M nằm bên trái trục tung.
Khi đó:\(\;\cos {120^o} = - \,\;\overline {ON} ,\;\;\sin {120^o} = \overline {OP} \)
Vì \(\widehat {xOM} = {120^o}\) nên \(\widehat {NOM} = {180^o} - {120^o} = {60^o}\) và \(\widehat {POM} = {120^o} - {90^o} = {30^o}\)
Vậy các tam giác \(\Delta MON\) và \(\Delta MOP\) vuông tại N, p và có một góc bằng \({30^o}\)
\( \Rightarrow ON = MP = \frac{1}{2}OM = \frac{1}{2}\)(Trong tam giác vuông, cạnh đối diện góc \({30^o}\) bằng một nửa cạnh huyền)
Và \(OP = MN = \sqrt {O{M^2} - O{N^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
Vậy điểm M có tọa độ là \(\left( { - \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\).
Và \(\cos {120^o} = - \frac{1}{2};\;\;\;\sin {120^o} = \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l}\; \Rightarrow \;\tan {120^o} = \frac{{\sin {{120}^o}}}{{\cos {{120}^o}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 ;\\\cot {120^o} = \frac{{\cos {{120}^o}}}{{\sin {{120}^o}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = \frac{{ - 1}}{{\sqrt 3 }} = - \frac{{\sqrt 3 }}{3}.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({120^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {120^o}\), bấm phím: sin 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 3 }}{2}\)
Tính \(\cos {120^o}\),bấm phím: cos 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{ - 1}}{2}\)
Tính \(\tan {120^o}\), bấm phím: tan 1 2 0 \(^o\)’’’ = ta được kết quả là \( - \sqrt 3 \)
( Để tính \(\cot {120^o}\), ta tính \(1:\tan {120^o}\))
Đúng 0
Bình luận (0)
Không dùng bảng số hay máy tính cầm tay, tính giá trị của các biểu thức sau:
a) \(\left( {2\sin {{30}^o} + \cos {{135}^o} - 3\tan {{150}^o}} \right).\left( {\cos {{180}^o} - \cot {{60}^o}} \right)\)
b) \({\sin ^2}{90^o} + {\cos ^2}{120^o} + {\cos ^2}{0^o} - {\tan ^2}60 + {\cot ^2}{135^o}\)
c) \(\cos {60^o}.\sin {30^o} + {\cos ^2}{30^o}\)
a)
Đặt \(A = \left( {2\sin {{30}^o} + \cos {{135}^o} - 3\tan {{150}^o}} \right).\left( {\cos {{180}^o} - \cot {{60}^o}} \right)\)
Ta có: \(\left\{ \begin{array}{l}\cos {135^o} = - \cos {45^o};\cos {180^o} = - \cos {0^o}\\\tan {150^o} = - \tan {30^o}\end{array} \right.\)
\( \Rightarrow A = \left( {2\sin {{30}^o} - \cos {{45}^o} + 3\tan {{30}^o}} \right).\left( { - \cos {0^o} - \cot {{60}^o}} \right)\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\left\{ \begin{array}{l}\sin {30^o} = \frac{1}{2};\tan {30^o} = \frac{{\sqrt 3 }}{3}\\\cos {45^o} = \frac{{\sqrt 2 }}{2};\cos {0^o} = 1;\cot {60^o} = \frac{{\sqrt 3 }}{3}\end{array} \right.\)
\( \Rightarrow A = \left( {2.\frac{1}{2} - \frac{{\sqrt 2 }}{2} + 3.\frac{{\sqrt 3 }}{3}} \right).\left( { - 1 - \frac{{\sqrt 3 }}{3}} \right)\)
\(\begin{array}{l} \Leftrightarrow A = - \left( {1 - \frac{{\sqrt 2 }}{2} + \sqrt 3 } \right).\left( {1 + \frac{{\sqrt 3 }}{3}} \right)\\ \Leftrightarrow A = - \frac{{2 - \sqrt 2 + 2\sqrt 3 }}{2}.\frac{{3 + \sqrt 3 }}{3}\\ \Leftrightarrow A = - \frac{{\left( {2 - \sqrt 2 + 2\sqrt 3 } \right)\left( {3 + \sqrt 3 } \right)}}{6}\\ \Leftrightarrow A = - \frac{{6 + 2\sqrt 3 - 3\sqrt 2 - \sqrt 6 + 6\sqrt 3 + 6}}{6}\\ \Leftrightarrow A = - \frac{{12 + 8\sqrt 3 - 3\sqrt 2 - \sqrt 6 }}{6}.\end{array}\)
b)
Đặt \(B = {\sin ^2}{90^o} + {\cos ^2}{120^o} + {\cos ^2}{0^o} - {\tan ^2}60 + {\cot ^2}{135^o}\)
Ta có: \(\left\{ \begin{array}{l}\cos {120^o} = - \cos {60^o}\\\cot {135^o} = - \cot {45^o}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}{120^o} = {\cos ^2}{60^o}\\{\cot ^2}{135^o} = {\cot ^2}{45^o}\end{array} \right.\)
\( \Rightarrow B = {\sin ^2}{90^o} + {\cos ^2}{60^o} + {\cos ^2}{0^o} - {\tan ^2}60 + {\cot ^2}{45^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\left\{ \begin{array}{l}\cos {0^o} = 1;\;\;\cot {45^o} = 1;\;\;\cos {60^o} = \frac{1}{2}\\\tan {60^o} = \sqrt 3 ;\;\;\sin {90^o} = 1\end{array} \right.\)
\( \Rightarrow B = {1^2} + {\left( {\frac{1}{2}} \right)^2} + {1^2} - {\left( {\sqrt 3 } \right)^2} + {1^2}\)
\( \Leftrightarrow B = 1 + \frac{1}{4} + 1 - 3 + 1 = \frac{1}{4}.\)
c
Đặt \(C = \cos {60^o}.\sin {30^o} + {\cos ^2}{30^o}\)
Sử dụng bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {30^o} = \frac{1}{2};\;\;\cos {30^o} = \frac{{\sqrt 3 }}{2};\;\cos {60^o} = \frac{1}{2}\;\)
\( \Rightarrow C = \frac{1}{2}.\frac{1}{2} + {\left( {\;\frac{{\sqrt 3 }}{2}} \right)^2} = \frac{1}{4} + \frac{3}{4} = 1.\)
Đúng 0
Bình luận (0)
Giá trị của các hàm số lượng giác
sin
5
π
4
,
sin
5
π
3
lần lượt bằng
Đọc tiếp
Giá trị của các hàm số lượng giác sin 5 π 4 , sin 5 π 3 lần lượt bằng
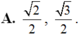
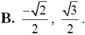
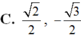
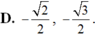
Không tính giá trị cụ thể, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự từ nhỏ đến lớn. sin
20
°
, cos
20
°
, sin
55
°
, cos
40
°
, tg
70
°
Đọc tiếp
Không tính giá trị cụ thể, hãy sắp xếp các tỉ số lượng giác sau theo thứ tự từ nhỏ đến lớn. sin 20 ° , cos 20 ° , sin 55 ° , cos 40 ° , tg 70 °
Để ý rằng với các góc nhọn, khi góc lớn lên thì sin của nó lớn lên và chú ý rằng cos 20 ° = sin 70 ° , cos 40 ° = sin 50 ° và do sin α < tg α từ
sin 20 ° < sin 50 ° (= cos 40 ° ) < sin 55 ° < sin 70 ° (= cos 20 ° ) < tg 70 ° .
Suy ra sin 20 ° < cos 40 ° < sin 55 ° < cos 20 ° < 70 °
Đúng 0
Bình luận (0)
Tìm các giá trị lượng giác còn lại biết:
a) Cho sin \(x=-\dfrac{4}{5}\)và \(90^o< x< 180^o\)
b) Cho \(\sin x=\dfrac{\sqrt{3}}{2}\)và \(270^o< x< 360^o\)
c) Cho \(\cos x=-\dfrac{1}{3}\)và \(0^o< x< 90^o\)
a: Sửa đề: sin x=4/5
cosx=-3/5; tan x=-4/3; cot x=-3/4
b: 270 độ<x<360 độ
=>cosx>0
=>cosx=1/2
tan x=căn 3; cot x=1/căn 3
Đúng 0
Bình luận (0)