Trong Ví dụ 3, hãy xác định giao tuyến của hai mặt phẳng (SBM) và (SCN).
Trong Ví dụ 3, hãy xác định giao tuyến của mặt phẳng (EMQ) và mặt phẳng (ABCD).
Ta có (MNPQ) // (ABCD) (chứng minh ở Ví dụ 2)
Vì vậy giao tuyến của (EMQ) với hai mặt phẳng (MNPQ) và (ABCD) song song với nhau
Trong mặt phẳng (EMQ), qua E vẽ đường thẳng ET // MQ (T thuộc CD)
Như vậy, đường thẳng ET là giao tuyến của (EMQ) và (ABCD).
Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)
Hai mp(SAD) và (SBC) có điểm chung S và chứa hai đường thẳng song song AD và BC.
Do đó, giao tuyến của hai mp(SAD) và (SBC) là đường thẳng n đi qua S song cong với AD và BC.
Trong Ví dụ 4, xác định giao tuyến của hai mặt phẳng (SAC) và (SBD).
Gọi O là giao điểm của AC và BD
Vì S và O cùng thuộc hai mặt phẳng (SAC) và (SBD)
Suy ra SO là giao tuyến của hai mặt phẳng (SAC) và (SBD)
Trong Ví dụ 4, gọi (Q) là mặt phẳng qua E và song song với hai đường thẳng AB, AD. Xác định giao tuyến của (Q) với các mặt của tứ diện.
Mặt phẳng (ABC) chứa đường thẳng AB song song với (Q) nên mp(ABC) cắt mp(Q) theo giao tuyến song song với AB. Vẽ EF // AB (F thuộc BC) thì EF là giao tuyến của (Q) và (ABC).
Hai mặt phẳng (ACD) và (ABD) cùng chứa đường thẳng AD song song với (Q) nên chúng cắt mặt phẳng (Q) theo giao tuyến song song với với AD. Vẽ EK song song với AD (K thuộc CD) thì EK, FK lần lượt là giao tuyến của mp(Q) với hai mp(ACD) và (BCD).
Trong Ví dụ 4, vẽ một đường thẳng c cắt cả hai đường thẳng a và b. Xác định giao tuyến của hai mặt phẳng: mp (S, a) và mp (S, c); mp (S, b) và mp (S, c).
Đường thẳng c cắt a, b lần lượng tại A và B.
Giao tuyến của mp(S,a) và mp(S,c) là SA.
Giao tuyến của mp(S,b) và mp(S,c) là SB.
Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD.
a) Tìm giao điểm N của đường thẳng CD và mp(SBM).
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC).
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC).
d) Tìm giao điểm P của SC và mặt phẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM).
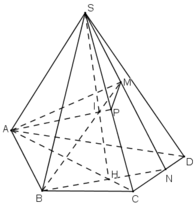
a) SM, CD cùng thuộc (SCD) và không song song.
Gọi N là giao điểm của SM và CD.
⇒ N ∈ CD và N ∈ SM
Mà SM ⊂ (SMB)
⇒ N ∈ (SMB)
⇒ N = (SMB) ∩ CD.
b) N ∈ CD ⊂ (ABCD)
⇒ BN ⊂ (ABCD)
⇒ AC; BN cùng nằm trong (ABCD) và không song song
Gọi giao điểm của AC và BN là H.
+ H ∈ AC ⊂ (SAC)
+ H ∈ BN ⊂ (SBM)
⇒ H ∈ (SAC) ∩ (SBM)
Dễ dàng nhận thấy giao điểm thứ hai của (SAC) và (SBM) là S
⇒ (SAC) ∩ (SBM) = SH.
c) Trong mp(SBM), gọi giao điểm của BM và SH là I, ta có:
I ∈ BM
I ∈ SH ⊂ (SAC).
⇒ I = BM ∩ (SAC).
) Trong mp(SAC), gọi giao điểm của AI và SC là P.
+ P ∈ AI, mà AI ⊂ (AMB) ⇒ P ∈ (AMB)
⇒ P = (AMB) ∩ SC.
Lại có P ∈ SC, mà SC ⊂ (SCD) ⇒ P ∈ (SCD).
⇒ P ∈ (AMB) ∩ (SCD).
Lại có: M ∈ (SCD) (gt)
⇒ M ∈ (MAB) ∩ (SCD)
Vậy giao điểm của (MAB) và (SCD) là đường thẳng MP.
Trong Ví dụ 6, xác định giao điểm của đường thẳng DF và mặt phẳng (ABC).
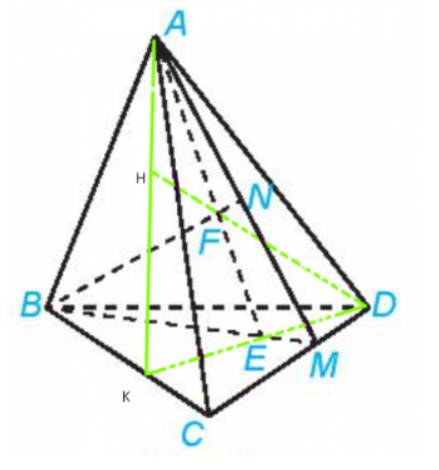
Xét trong mp(BCD) ta có: DE cắt BC tại K.
Xét trong mp(ADK) ta có: AF cắt AK tại H.
Như vậy, H thuộc đường thẳng DF và AK mà AK nằm trong mp(ABC) suy ra H cũng nằm trong mp(ABC).
Do đó, H là giao điểm của DF và mp(ABC).
Cho hình chóp S.ABCD có AB và CD không song song. Gọi M là một điểm thuộc miền trong của tam giác SCD
a) Tìm giao điểm N của đường thẳng CD và mặt phẳng (SBM)
b) Tìm giao tuyến của hai mặt phẳng (SBM) và (SAC)
c) Tìm giao điểm I của đường thẳng BM và mặt phẳng (SAC)
d) Tìm giao điểm P của SC và mặt phẳng (ABM), từ đó suy ra giao tuyến của hai mặt phẳng (SCD) và (ABM)
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ.
Ví dụ 2: Cho tử diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh BC và AC. Trên cạnh DB lấy điểm P sao cho DP = 2PB . a). Xác định giao tuyến của mặt phẳng (MNP) với các mặt phẳng (ABD),(BCD).