Độ dài đèo Hải Vân là:

\(6,28:\frac{{157}}{{500}} = \frac{{157}}{{25}}.\frac{{500}}{{157}} = \frac{{3135}}{{157}} \approx 20\,\left( {km} \right)\)

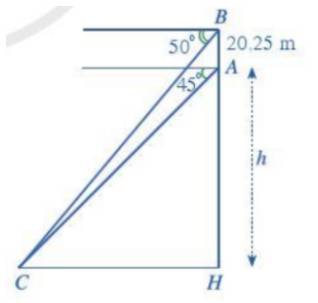
\(\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.\) (hai góc đồng vị)

Mà \(\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h\)

Lại có: \(\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}\)

\(\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}\)

Vậy chiều cao của đỉnh Lũng cú so với chân núi là khoảng 105,6m.

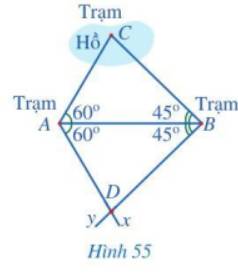
Xét hai tam giác ABC và ABD có: \(\widehat {CAB} = \widehat {DAB} = 60^\circ ,\widehat {ABC} = \widehat {ABD} = 45^\circ \), AB chung.

Vậy \(\Delta ABC = \Delta ABD\) (g.c.g). 

Suy ra AC = AD và BC = BD ( 2 cạnh tương ứng)

Góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất) là góc \(\widehat B\).

Ta có:

\(\widehat B + 90^\circ  + 18^\circ  = 180^\circ \) (tổng ba góc của một tam giác).

Suy ra: \(\widehat B = 180^\circ  - 90^\circ  - 18^\circ  = 72^\circ \)

Vậy góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang có số đo là 72°.

Ta có: \(f\left( t \right) = {f_1}\left( t \right) + {f_2}\left( t \right) = 5\sin t + 5\cos t = 5\left( {\sin t + \cos t} \right) = 5\sqrt 2 \sin \left( {t + \frac{\pi }{4}} \right)\)

Suy ra: \(k = 5\sqrt 2 ,\;\varphi  = \frac{\pi }{4}\).

Ta có \(P\left( F \right) = \frac{{n\left( F \right)}}{{n\left( \Omega  \right)}} = \frac{1}{{C_{45}^6}} = \frac{1}{{8145060}}\) và \(P\left( G \right) = \frac{{n\left( G \right)}}{{n\left( \Omega  \right)}} = \frac{{234}}{{C_{45}^6}} = \frac{{39}}{{1357510}}\).

Bạn ấy áp dụng hđt hiệu hai bình phương

+) Vệ tinh cách mặt đất 1 000 km thì h=1 000

Khi đó

 \(\begin{array}{l}1000 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = 1\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = \cos 0\\ \Leftrightarrow \frac{\pi }{{50}}t = 0 + k2\pi \\ \Leftrightarrow t = 100.k\,\,\,\,;k \in N*\end{array}\)

+) Vệ tinh cách mặt đất 250 km thì h=250

Khi đó

 \(\begin{array}{l}250 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t =  - \frac{2}{3}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{50}}t = \arccos \left( { - \frac{2}{3}} \right) + k2\pi \\\frac{\pi }{{50}}t =  - \arccos \left( { - \frac{2}{3}} \right) + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{50}}{\pi }\left[ {\arccos \left( { - \frac{2}{3}} \right) + k2\pi } \right]\\t = \frac{{50}}{\pi }\left[ { - \arccos \left( { - \frac{2}{3}} \right) + k2\pi } \right]\end{array} \right.;k \in N*\end{array}\)

+) Vệ tinh cách mặt đất 100 km thì h=100

Khi đó

\(\begin{array}{l}100 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t =  - 1\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = \cos \pi \\ \Leftrightarrow \frac{\pi }{{50}}t = \pi  + k2\pi \\ \Leftrightarrow t = 50 + 100k\,\,\,\,;k \in N*\end{array}\)

Để ống đựng nước cách mặt nước 2m thì \(h = \left| y \right| = 2\)

Hay \(\left| {2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2} \right| = 2\)

Suy ra \(2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2 = 2\) hoặc \(2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2 =  - 2\)

*) \(2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2 = 2\\ \Leftrightarrow \sin \left( {2\pi x - \frac{\pi }{2}} \right) = 0\\ \Leftrightarrow 2\pi x - \frac{\pi }{2} = k\pi ,k \in Z\\ \Leftrightarrow 2x - \frac{1}{2} = k,k \in Z\\ \Leftrightarrow x = \frac{{2k + 1}}{4},k \in Z\\ \Leftrightarrow x \in \left\{ {....; - \frac{1}{4};\frac{1}{4};\frac{3}{4};....} \right\}\)

*)\(2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2 =  - 2\\ \Leftrightarrow \sin \left( {2\pi x - \frac{\pi }{2}} \right) =  - 1,6\, <  - 1\)

Vì tập giá trị của hàm số sin là \(\left[ { - 1;1} \right]\) nên trong trường hợp này phương trình vô nghiệm.