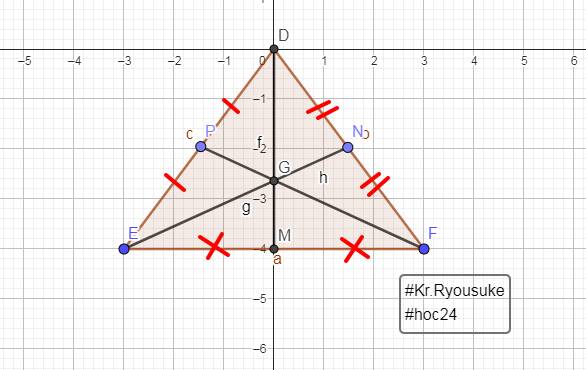
Trong Hình 3, hãy vẽ các đường phân giác GM, EN và FP của tam giác EFG.

Những câu hỏi liên quan
Các phân giác ngoài của tam giác abc cắt nhau và tạo thành tam giá efg.
a. Tính các góc cửa tam giác efg theo tam giác abc
b. Chứng minh rằng các phân giác trong của tam giác abc đi qua các đỉnh efg
Tam giác DEF có các đường trung tuyến DM, EN và FP cắt nhau tại G. Khẳng định nào sau đây là sai? A. GD = 2GM . B. EN = 3NG . C. GF/FP = 1/3 . D. EG/EN = 2/3 ( help me please )
`\Delta DEF` có:
\(\text{DM}\cap\text{EN}\cap\text{FP}=\text{G}\)
Mà \(\text{DM, EN, FP}\) là các đường trung tuyến
`->`\(\text{G là trọng tâm của }\Delta\text{DEF}\)
A. `GD = 2GM` (đúng)
B. EN = 3GN (đúng)
C. `(GF)/(FP)=1/3` (sai)
`-` Khoảng cách từ trọng tâm đến đỉnh là `2/3` chứ không phải `1/3`.
D. `(EG)/(EN) = 2/3` (đúng)
Xét các đáp án trên `-> C (tm).`
Đúng 1
Bình luận (0)
Các phân giác ngoài của tam giác ABC cắt nhau tạo thành tam giác EFG. Tỉnh các góc của tam giác EFG theo các góc của tam giác ABC
cho tam giác MNP, vẽ trung tuyến NE VÀ PF. trên tia đối của tia EN VÀ FP lần lượt lấy hai điểm K, H sao cho EK=EN, FH=FP.
a) cm tam giác EMK=ENP; FMH=FNP
b) cm ba điểm H, M, K Thẳng hàng
c) HK=2NP
Cho hình vẽ bên , biết diện tích tam giác MEG bằng diện tích tam giác GEN . Hãy so sánh GM và GN
ok mik sẽ gửi
Vẽ một tam giác trên giấy. Cắt rời tam giác ra khỏi tờ giấy rồi gấp hình tam giác đó để xác định ba đường phân giác của tam giác (Hình 4). Em hãy quan sát và nhận xét xem ba đường phân giác có cùng đi qua một điểm không.
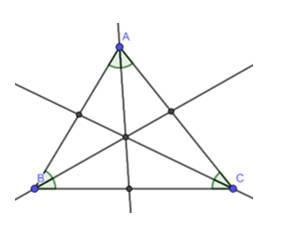
Ta thấy 3 tia phân giác của tam giác cùng đi qua 1 điểm
Đúng 0
Bình luận (0)
Các phân giác ngoài của tam giác ABC cắt nhau tạo thành tam giác AFG.
a, tính các góc của tam giác EFG theo góc của tam giác ABC
b, CMR: các phân giác trong của ABCđi qua các điểm E,F,G.
Cho tam giác EFG vuông tại F có FG=3cm,EG=4cm a) giải tam giác vuông EFG b) phân giác của góc E cắt FG tại H. Tính GF; GH C) từ H kẻ HM và HN lần lượt vuông góc với EF và EG . Tam giác EMNHN là hình gì ? Tính chu vi và diện tích củ tam giác . EMNHN các góc làm tròn đến phút cạch làm tròn đến chữ số thập phân thứ 3
Mn giúp em vs ạ ^^
c) Xét tứ giác FMHN có
\(\widehat{NFM}=90^0\)
\(\widehat{FNH}=90^0\)
\(\widehat{FMH}=90^0\)
Do đó: FMHN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Hình chữ nhật FMHN có đường chéo FH là tia phân giác của \(\widehat{NFM}\)(gt)
nên FMHN là hình vuông(Dấu hiệu nhận biết hình vuông)
Đúng 0
Bình luận (0)
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.
Tham khảo:
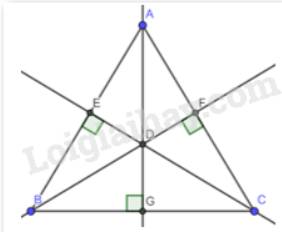
Nhận xét: Các đường cao cùng đi qua 1 điểm
Đúng 0
Bình luận (0)

















