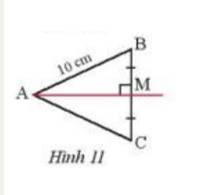
Quan sát Hình 11, cho biết M là trung điểm của BC, AM vuông góc với BC và AB = 10 cm, Tính AC.
Những câu hỏi liên quan
Cho tam giác abc cân tại a . M là trung điểm của bc . Mi vuông góc vs ab . Mk vuông góc vs ac. - chứng minh tam giác BIM = tam giác BKM - chứng minh AM là đường trung trực của BC - Tính BC biết Ab = 10 cm , AM =8cm
a)
Sửa đề: ΔBIM=ΔCKM
Xét ΔBIM vuông tại I và ΔCKM vuông tại K có
BM=CM(M là trung điểm của BC)
\(\widehat{IBM}=\widehat{KCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔBIM=ΔCKM(cạnh huyền-góc nhọn)
Đúng 1
Bình luận (1)
1. Cho tam giác ABC vuông tại A gọi M là trung điểm của BC trên tia AM lấy E sao cho M là trung điểm của AE
a) CM: AB vuông góc với AE
b) CM: AM=1/2 BC
c) Tính AE biết AB=3cm, AC=4cm
Trên nửa mặt phẳng bờ là đường thẳng đi qua hai điểm B, C. Vẽ tia Bx sao cho góc CBx = 70 độ, vẽ tia Cy sao cho góc BCy = 110 độ
a) Chỉ ra các cặp góc bù nhau
b) Qua hình vẽ, dự đoán gì về 2 tia Bx, Cy ?
LÀM HỘ EM ĐƯỢC KHÔNG Ạ ? EM CẢM ƠN NHIỀU Ạ
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, biết AB=6cm ,AC=8cm. Gọi M là trung điểm của đoạn thẳng BC
a, Tính độ dài BC,AM
b, Kẻ MDvuong góc AB (Dthuoc AB) ME vuông góc AC ( E thuoc AC) . Tứ giác ADME là hình gì?
c, Tam giác ABC có đk gì để tứ giác ADME là hình vuông ?
d, Gọi F đx với A qua M . Kể FH vuông góc vs BC ( H thuộc BC ) Gọi K là trung điểm của BH. CM : FK vuông góc vs EK ?
) Cho ABC vuông tại A, M là trung điểm của BC. Biết BC = 10 (cm)
Từ M kẻ ME vuông góc AB tại E (E e AB) và MF vuông góc AC tại F (F e AC)
a) Vẽ hình, ghi giả thiết kết luận.
b) Tính AM.
c) Chứng minh AEMF là hình chữ nhật
a,
GT KL tự làm
b, AM=1/2BC=5cm
c,Xét tứ giác AEMF có 3 góc :\(MEA=EAF=AFM=90^o\)
do đó đó AEMF là hình chữ nhật
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A (AC>AB). M là trung điểm của BC, qua M kẻ Me vuông góc với AB tại E, MF vuông góc với AC tại F
a/ AEMF là hình gì
b/ Cho biết E và F là trung điểm của AB và AC. chứng minh BÈC là hình thang
c/ giả sử góc B=60 độ, BC=24cm. Tính AM và chu vi tam giác AMB
d/ kẻ AH vuông góc với BC tại H, chứng minh góc EHF=90 độ
Ta có AB vuông góc với AC, MF vuông góc với AC suy ra MF song song với AB, xét tam giácBca có m là trung điểm của BC, MF song song với AB suy ra ra f là trung điểm của AC mà f là trung điểm của mn suy ra m n cắt AC tại f suy ra tứ giác mcna là hình bình hành
Cho tam giác ABC cân tại A, trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD=AE. Gọi M là giao điểm của BE và CD. Cmr:
a. BE=CD
b. tam giác BMD=CME
c. AM là p/g góc BAC
d. Cm: DE // BC
e. Gọi O là giao điểm của AM và BC. Cm: AM vuông góc BC. M là trung điểm BC. Tính AO biết BC=12cm, ab=10cm
g. Kẻ BH vuông góc AC. Cmr: AB^2 + AC^2 + BC^2 = CH^2 + 2AH^2 + BH^2
GIÚP MÌNH CÂU G VỚI
Cho tam giác ABC vuông tại A có AB<AC. Gọi M Là trung điểm của BC, kẻ MD vuông góc với AB tại D, ME vuông góc với AC tại E
a) Cm AM=DE
b) Cm tứ giác DMCE là hbh
c) Gọi AH là đường cao của tam giác ABC (H thuộc BC). Cm tứ giác DHME là hình thang cân và DE là trung trực của AH
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
=>AM=DE
b: Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình
=>DE//BC và DE=1/2BC
=>DE//MC và DE=MC
Xét tứ giác DMCE có
DE//MC
DE=MC
Do đó: DMCE là hình bình hành
c: ΔHAC vuông tại H có HE là trung tuyến
nên \(HE=\dfrac{1}{2}AC\)
mà \(MD=\dfrac{1}{2}AC\)
nên HE=MD
Xét tứ giác DHME có
ED//MH
nên DHME là hình thang
mà HE=MD
nên DHME là hình thang cân
ΔHAB vuông tại H
mà HD là trung tuyến
nên HD=AD
EA=EH
DA=DH
Do đó: ED là đường trung trực của AH
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB<AC, đường cao AH, từ H kẻ HD vuông góc với AB, HE vuông góc với AC. M là trung điểm
a) Chứng minh tứ giác ADHE là hình chữ nhật
b) Biết AM bằng 5cm, HM bằng 3 cm. Hãy tính AH,BC và diện tích ABC
c) Chứng minh AM vuông góc với DE
P/s: Mình biết làm 2 câu trên rồi, quan trọng là câu c) á. Cám Ơn nhiều
(1đ) Cho ABC vuông tại A. M là trung điểm của BC. Biết BC 10 (cm) Iét Mike MẸ vuông góc AB tại E (E = AB) và MF vuông góc AC tại F (F = AC) a) Về hình, chỉ giả thiết kết luận