Hãy nhắc lại cách nhân hai đơn thức và tính (12x3).(-5x2)

Những câu hỏi liên quan
Hãy nhắc lại công thức tính khoảng cách giữa 2 điểm \(I\left( {a;b} \right)\) và \(M\left( {x;y} \right)\)trong mặt phẳng Oxy.
Khoảng cách hai điểm M,I (hay độ dài đoạn thẳng MI) chính là độ dài vecto \(\overrightarrow {MI} \)
\(\overrightarrow {MI} = \left( {a - x;b - y} \right) \Rightarrow \left| {\overrightarrow {MI} } \right| = \sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
Vậy khoảng cách giữa hai điểm \(I\left( {a;b} \right)\) và \(M\left( {x;y} \right)\) là \(\sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
Đúng 0
Bình luận (0)
cách làm bài này theo nhân đơn thức với đa thức như thế nào 8x.(x-2)-3.(x2-4x-5)-5x2
\(8x\left(x-2\right)-3\left(x^2-4x-5\right)-5x^2\)
\(=8x^2-16x-3x^2+12x+15-5x^2\)
\(=15-4x\)
`8x(x-2) -3 (x^2 -4x-5)-5x^2`
`= 8x^2 - 16x - 3x^2 +12x+15 - 5x^2`
`= (8x^2 - 3x^2 - 5x^2)+(-16x +12x)+15`
`= -4x +15`
Câu 15A. giữa hai dấu gạch ngang. B. Nhắc lại nguyên văn lời nói hay ý nghĩ của ngưởi hoặc nhân vật và đặt trong dấu ngoặc . D. sau dấu hai chấm Trong đoạn trích Chị em Thúy Kiều, câu thơ “Mai cốt cách, tuyết tinh thần” gợi tả gì? Gợi vẻ đẹp duyên dáng, thanh cao, trong trắng của chị em Kiều
Đọc tiếp
Câu 15

A. giữa hai dấu gạch ngang. B. Nhắc lại nguyên văn lời nói hay ý nghĩ của ngưởi hoặc nhân vật và đặt trong dấu ngoặc . D. sau dấu hai chấm Trong đoạn trích Chị em Thúy Kiều, câu thơ “Mai cốt cách, tuyết tinh thần” gợi tả gì? Hãy nhắc lại: a) Các hằng đẳng thức lượng giác cơ bản; b) Công thức cộng; c) Công thức nhân đôi; d) Công thức biến đổi tích thành tổng và tổng thành tích. a) Các hằng đẳng thức lượng giác cơ bản: sin2α + cos2α = 1 1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z 1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z tanα.cotα = 1; α ≠ kπ/2, k ∈ Z b) Công thức cộng: cos(a - b) = cosa cosb + sina sinb cos(a + b) = cosa cosb - sina sinb sin(a - b) = sina cosb - cosa sinb sin(a + b) = sina.cosb + cosa.sinb c) Công thức nhân đôi: sin2α = 2 sinα cosα cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α d) Công thức biến đổi tích thành tổng: cos a cosb = 1/2 [cos(a - b) + cos(a + b) ] sina sinb = 1/2 [cos(a - b) - cos(a + b) ] sina cosb = 1/2 [sin(a - b) + sin(a + b) ] Công thức biến đổi tổng thành tích: *Dạng 1: Nhân đơn thức với đa thức; nhân đa thức với đã thức:
Hãy điền vào chỗ trống (...) để được đẳng thức hoàn chỉnh: 1) A.(B+C) = A.B + A.C
2) (A + B).(C + D) = A.C + A.D + B.C + B.D
BT: Làm tình nhân:
(1) 5x2 (3x2 - 7x + 2);
(2) (x + 3)(x2 + 3x - 5) 2: \(=x^3+3x^2-5x+3x^2+9x-15\) \(=x^3+6x^2+4x-15\) Tìm thương của mỗi phép chia sau: a) 12x3 : 4x b) (-2x4) : x4 c) 2x5 : 5x2 a) 12x3 : 4x = (12:4) . (x3 : x) = 3.x2 b) (-2x4 ) : x4 = [(-2) : 1] . (x4 : x4) = -2 c) 2x5 : 5x2 = (2:5) . (x5 : x2) = \(\frac{2}{5}\)x3 Cho hai đơn thức
A
(
x
)
=
-
2
x
3
+
9
-
6
x
+
7
x
4
-
2
x
2
,
B
(
x
)
=
5
x
2
+
9
x
-
3
x
4
+
7
x
3
-
12
.
Tính tổng A(x) + B(x) của hai đa thức A.
4
x
4
-
5
x
3
+
3
x
2
+
3
x
+
3
B.
4
x
4
+
5
x
3
+
3
x
2
+
3
x
-
3
C.
-
2
x
4
+
5
x
3
-
3
x
2
+
3
x
-
3
D.
7
x
4
+
5
x
3
+
3
x
2
-
3
x
-
3
Ta có: A(x) + B(x) = -2x3 + 9 - 6x + 7x4 - 2x2+ 5x2 + 9x - 3x4 + 7x3 - 12 = 4x4 + 5x3 + 3x2 + 3x - 3. Chọn B Hãy nhắc lại công thức tính thể tích khối lăng trụ có diện tích đáy bằng B và chiều cao bằng h. Công thức tính thể tích lăng trụ có diện tích đáy là B và chiều cao là h là: V = B*h Hãy nhắc lại định lí côsin trong tam giác. Từ các hệ thức này hãy tính cosA, cosB và cosC theo các cạnh của tam giác ? Định lí: Trong một tam giác bất kì, bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với cosin của góc xen giữa chúng. Ta có các hệ thức sau: a2 = b2 + c2 - 2bc.cosA (1) b2 = a2 + c2 - 2bc.cosB (2) c2 = a2 + b2 - 2bc.cosC (3) Hệ quả: Từ định lí cosin suy ra: cosA = cosC = Gợi vẻ đẹp duyên dáng, thanh cao, trong trắng của chị em Kiều
Xem chi tiết
Xem chi tiết
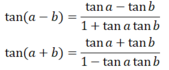
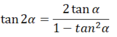
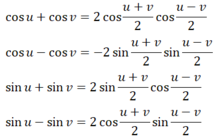 Đúng 0
Bình luận (0)
Xem chi tiết
Đúng 2
Bình luận (0)
Xem chi tiết
Đúng 1
Bình luận (0)
Xem chi tiết
Cho hai đơn thức
A
(
x
)
-
2
x
3
+
9
-
6
x
+
7
x
4
-
2
x
2
,
B
(
x
)
5
x
2
+
9
x
-
3
x
4
+
7
x
3
-
12
.
Tính tổng...Đọc tiếp
Đúng 0
Bình luận (0)
Xem chi tiết
Đúng 0
Bình luận (0)
Xem chi tiết
Đúng 0
Bình luận (0)
Xem chi tiết
Đúng 2
Bình luận (0)
Xem chi tiết
Đúng 1
Bình luận (0)
Xem chi tiết
Cho hai đơn thức
A
(
x
)
-
2
x
3
+
9
-
6
x
+
7
x
4
-
2
x
2
,
B
(
x
)
5
x
2
+
9
x
-
3
x
4
+
7
x
3
-
12
.
Tính tổng...Đọc tiếp
Đúng 0
Bình luận (0)
Xem chi tiết
Đúng 0
Bình luận (0)
Xem chi tiết
cosB =
Đúng 0
Bình luận (0)
Khoá học trên OLM (olm.vn)














