Cho tam giác ABC vuông tại A, đg cao AH. Gọi E và F lần lượt là hình chiếu của H trên AB,AC
a. AE.AB=AF.AC
b.BE.AB=CF.AC=AH4
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có đường cao AH . Gọi E,F lần lượt là hình chiếu của H AB và AC
a) Chứng minh AE.AB=AF.AC
b) Tính M,biết M=5.sin2C+5.sin2B+2tanB tanC
a: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF vuông góc AC
nên AF*AC=AH^2
=>AE*AB=AF*AC
b: M=5*sin^2C+5*cos^2C+2*tanB*cot B
=5+2
=7
Đúng 1
Bình luận (1)
tam giác abc vuông tại a,ah vuông góc bc,e,f lần lượt là hình chiếu của h trên ab,ac
a)cm tam giác abc đồng dạng tam giác hba và ab2=bc.bh
b)cm ah2=ab.ab và ae.ab=af.ac
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: ΔAHB vuông tại H có HE là đường cao
nên AH^2=AE*AB
ΔAHC vuông tại H có HF là đường cao
nên AH^2=AF*AC
=>AE*AB=AF*AC
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A ,kẻ đường cao AH .gọi E,F lần lượt là hình chiếu của H lên AB và ACa) CMR :tứ giác AEHF là hình chữ nhật b) AE.AB=AF .ACc) đương thăng rđi qua A vuông góc với EF cắt BC tại i CMR :i là trung điểm của BC
tam giác ABC vuông tại A, đường cao AH. biết AB=9cm, AC= 12cm. Gọi E và F lần lượt là hình chiếu của H trên AB và AC.CM: AE.AB=AF.AC
cho tam giác ABC vuông tại A, đường cao AH, có BH=2cm, BC=8cm
A)tính AB, góc C
B)gọi E,F lần lượt là hình chiếu vuông tại H trên AB,AC. chứng minh BE.AB+CF.AC+HB.2HC+BC^2
C) Tìm diện tích tứ giác AEHF
a: CH=6cm
\(AB=\sqrt{BH\cdot BC}=4\left(cm\right)\)
\(\widehat{C}=30^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao AH. Gọi E và F lần lượt là hình chiếu của H trên AB và AC. Chứng minh rằng:
a) AEHF là hình chữ nhật .
b) AE.AB=AF.AC
b) Theo hệ thức lượng: AE.AB = AH2 ; AF.AC = AH2 => AE.AB = AF.AC.
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có ABAC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC. a/ chứng minh: tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB^2 BC.CHb/ Chứng minh: AE.ABAF.ACC/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCAMỌI NGƯỜI GIÚP MÌNH VỚI Ạ!!!
Đọc tiếp
cho tam giác ABC vuông tại A có AB<AC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC.
a/ chứng minh: tam giác ABC đồng dạng với tam giác HBA từ đó suy ra AB^2= BC.CH
b/ Chứng minh: AE.AB=AF.AC
C/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCA
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ!!!
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng vơi ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A có ABAC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC. a/ chứng minh: tam giác ABC đồng dạng với tam giác HCA từ đó suy ra AB^2 BC.CHb/ Chứng minh: AE.ABAF.ACC/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCAMỌI NGƯỜI GIÚP MÌNH VỚI Ạ
Đọc tiếp
cho tam giác ABC vuông tại A có AB<AC . Kẻ đường cao AH . E,F lần lượt là hình chiếu của điểm H trên AB và AC.
a/ chứng minh: tam giác ABC đồng dạng với tam giác HCA từ đó suy ra AB^2= BC.CH
b/ Chứng minh: AE.AB=AF.AC
C/Gọi O là trung điểm của BC . Qua H kẻ đường thẳng song song với EF cắt AC tại M. K là giao điểm của AO với HM. Chứng minh: tam giác KAM đồng dạng với tam giác HCA
MỌI NGƯỜI GIÚP MÌNH VỚI Ạ
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC. a) Viết tỉ số lượng giác góc B của AABC. b) Cho AB=6cm, AC = 8cm . Tính BC,AH c ) Chứng minh: AE.AB = AF AC
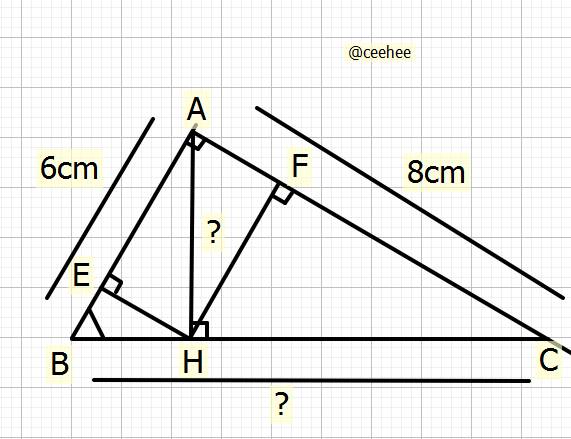
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)
Đúng 1
Bình luận (0)