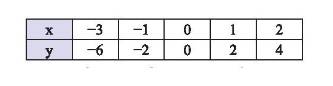
Vẽ đồ thị hàm số được cho bởi bảng sau:
Bài 1: cho hàm số y=f(x)=ax, biết đồ thị của hàm số đi qua điểm A(2;1) (vẽ đồ thị hàm số hộ mình)
a) Hãy xác định hệ số a
b) Tính f(-2); f(4); f(0)
Bài 2: Thời gian làm một bài tập Toán của một số học sinh lớp 7 (tính bằng phút) được thống kê bởi bảng sau:
5 6 7 4 5 6
5 8 8 8 9 7
6 5 5 5 4 10
a) Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b) Lập bảng Tần số. Tính số trung bình công?
c) Tìm Mốt của dấu hiệu?
Bài 1:
a: Thay x=2 và y=1 vào y=ax, ta được: 2a=1
hay a=1/2
Vậy: f(x)=1/2x
b: f(-2)=1/2x(-2)=-1
f(4)=1/2x4=2
f(0)=0
Cho hàm số f(x) liên tục trên ℝ có đồ thị như hình vẽ. Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số f (x) trục hoành và trục tung. Khẳng định nào sau đây đúng
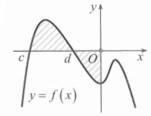
A. S = ∫ c d f x dx - ∫ d 0 f x dx
B. S = - ∫ c d f x dx - ∫ d 0 f x dx
C. S = - ∫ c d f x dx + ∫ d 0 f x dx
D. S = ∫ c d f x dx + ∫ d 0 f x dx
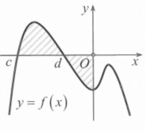
Cho hàm số f(x) liên tục trên R có đồ thị như hình vẽ. Gọi S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số f(x) trục hoành và trục tung. Khẳng định nào sau đây đúng:
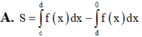
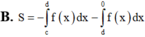
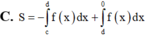
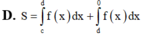
Cho hàm số bậc hai y = f x = x 4 − 5 x 2 + 4 có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f x và trục hoành (miền phẳng được tô đậm trên hình vẽ). Mệnh đề nào sau đây sai?
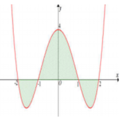
A. S = ∫ − 2 2 f x d x
B. S = 2 ∫ 0 2 f x d x
C. S = 2 ∫ 0 1 f x d x + 2 ∫ 1 2 f x d x
D. S = 2 ∫ 0 2 f x d x
D
Từ đồ thị của hàm số đối xứng qua trục tung nên đáp án A và B đúng.
Do ∫ 0 2 f x d x = ∫ 0 1 f x d x + − ∫ 1 2 f x d x
= ∫ 0 1 f x d x + − ∫ 1 2 f x d x
Nên đáp án C đúng. Vậy chọn đáp án D
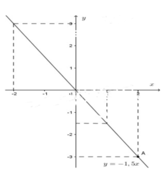
Hàm số y = f(x) được cho bởi công thức y = -1,5x. Vẽ đồ thị của hàm số trên
Vẽ hệ trục tọa độ Oxy
Với x= 2 ta được y = -3; điểm A(2; -3) thuộc đồ thị hàm số y = -1,5x.
Vậy đường thẳng OA là đồ thị của hàm số đã cho.
Bài 2: : Cho hàm số y= -2x +8
a. Vẽ đồ thị hàm số
b. Tính góc tạo bởi đồ thị hàm số với trục ox?
c. Tính khoảng cách từ gốc tọa độ đến đồ thị hàm số?
d. Điểm A(-1; 10 ) có thuộc đồ thị hàm số không?
e. Tính diện tích và chu vi của hình tạo bởi đồ thị hàm số với hai
trục tọa độ?
Cho hàm số y = f(x) và hàm số bậc ba y = g(x) có đồ thị như hình vẽ bên. Diện tích phần gạch chéo được tính bởi công thức nào sau đây?
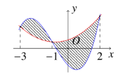
A . S = ∫ - 3 - 1 [ f ( x ) - g ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
B . S = | ∫ - 3 2 [ f ( x ) - g ( x ) ] dx |
C. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ f ( x ) - g ( x ) ] dx
D. S = ∫ - 3 - 1 [ g ( x ) - f ( x ) ] dx + ∫ - 1 2 [ g ( x ) - f ( x ) ] dx
Cho hàm số bậc nhất y = (2m – 1)x + m – 1, với m là tham số.
a) Khi m = 2, vẽ đồ thị của hàm số thu được và tính diện tích tam giác tạo bởi đồ thị và hai trục toạ độ. Gọi đường thẳng đó là (d1)
b) Khi m = - 1, vẽ đồ thị là đường thẳng (d2) của hàm số. Tính khoảng cách từ gốc toạ độ O đến đường thẳng (d2).
c) Chứng minh rằng khi m thay đổi thì các đường thẳng thu được luôn cùng đi qua
một điểm cố định.
Biết đồ thị hàm số bậc bốn y=f(x) được cho bởi hình vẽ bên dưới. Tìm số giao điểm của đồ thị hàm số y=g(x)= [f’(x)]2 – f(x). f’’(x) và trục hoành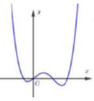
A. 4
B. 0.
C. 6.
D. 2.