Hình có rồi nên khỏi vẽ lại ạ
Những câu hỏi liên quan
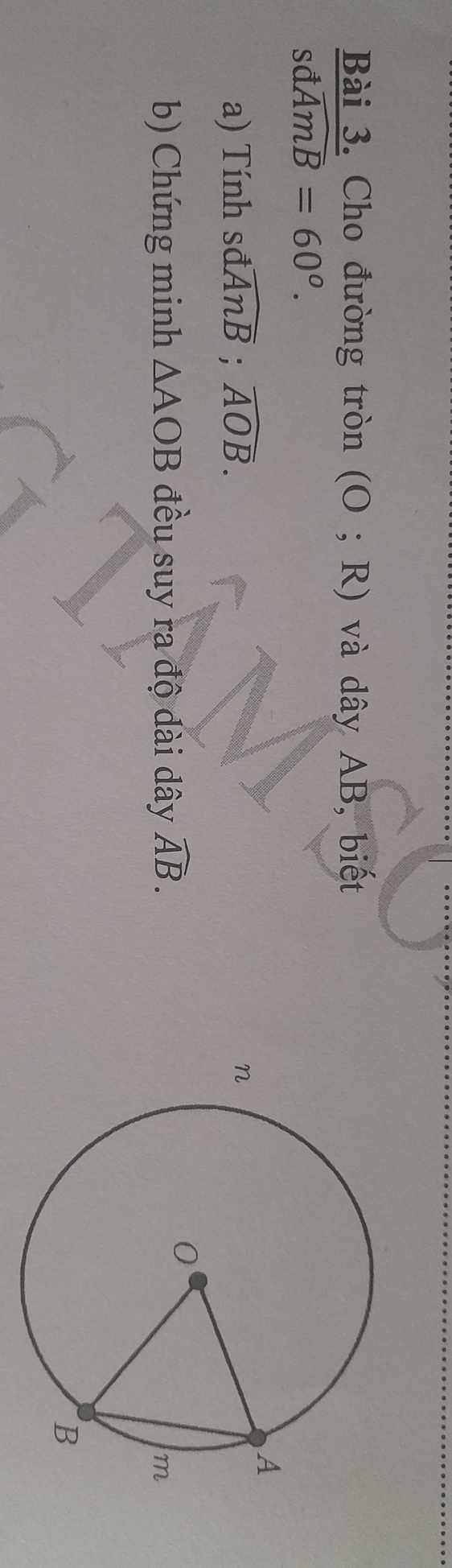
Hình có rồi nên khỏi vẽ lại ạ
a: Xét ΔOMN có OM=ON và góc MON=60 độ
nên ΔOMN đều
b: góc MON=60 độ
=>sđ cung nhỏ MN=60 độ
sđ cung lớn MN là:
360-60=300 độ
Đúng 0
Bình luận (0)
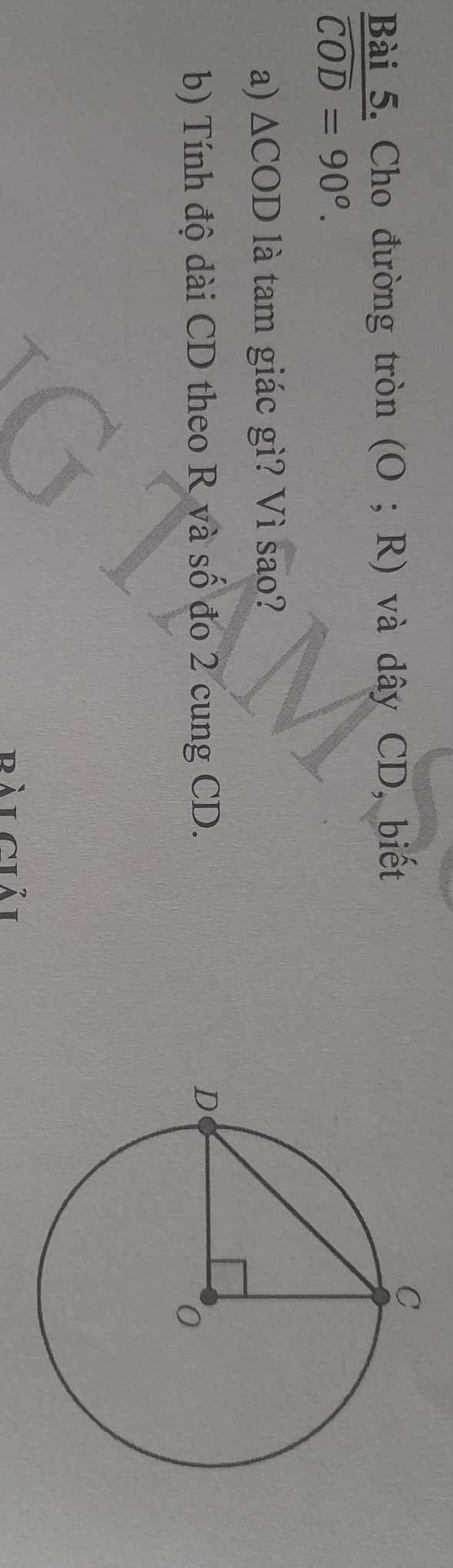
Hình có rồi khỏi vẽ lại ạ
a: Xét ΔOCD có OC=OD và \(\widehat{COD}=90^0\)
nên ΔOCD vuông cân tại O
b: \(\widehat{COD}=90^0\)
=>sđ cung nhỏ CD=90 độ
sđ cung lớn CD là: 360-90=270 độ
ΔOCD vuông tại O
=>\(CD^2=OC^2+OD^2=2R^2\)
=>\(CD=R\sqrt{2}\)
Đúng 0
Bình luận (0)
cách vẽ 5 hình tròn lập nhau trong logo,mai mình thi rồi nên mong mọi người giải nhanh chút ạ.
https://i.ytimg.com/vi/QUZpV-7wRPI/maxresdefault.jpg ( m.n xem hình , ảnh trên mạng nên hơi mờ ạ.)
edit "hinhtron": ARC 360 50
lệnh: repeat 6[ hinhtron rt 360/ 6]
cái thủ tục hình tròn là lệnh nâng cao nha bạn, nếu ko được thì dùng lệnh thường cũng được nha
Đúng 1
Bình luận (0)
6 tháng 4 2022 lúc 17:55
Tính giúp mình câu này với ạ. Btw, mình đã làm kiểm tra rồi nên chỉ check lại thôi nên không có gian lận gì đâu ạ
Cho tam giác nhọn ABC. Vẽ về phía ngoài tam giác các tam giác ABD; ACE vuông cân tại A. Vẽ đường cao AH của tam giác ABC. C/m AH đi qua trung điểm O của DE
Giúp tớ với... tớ cần lắm ạ..
Khỏi vẽ hình cx đc ạ... tớ vẽ rồi nhưng ko biết cách giải
Cho mình hỏi chút ạ, nếu như vẽ hình sai- ý sai ở đây là trong tam giác vuông tại A đáng lẽ AB>AC nhưng mik lại vẽ AB<AC . Nhưng kiểu hình vẫn đúng nên chứng minh vẫn đúng thì liệu bài hình đó còn được tính điểm không ạ?
có ai chuyên làm hoạt hình trên máy tính ko ạ?
mk bt là câu hỏi lihtih rồi khỏi khuyên nhé!
Câu lên trên mạng mà tìm phần mềm nhé
Đúng 0
Bình luận (0)
uk nhưng phải trao đổi vs 1 bn ms hỉu đc chứ !
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
27 tháng 2 2022 lúc 10:57
Cho ΔABC vuông tại A có AB = 3cm; BC = 5cm. Gọi CD là đường phân giác của ΔABC. Tính AC; BD và CD. (khỏi vẽ hình ạ)
Xét tam giác vuông ABC có:
\(AB^2+AC^2=BC^2\\ =>3^2+AC^2=5^2\\ =>AC^2=16\\ =>AC=4cm\)
Đúng 4
Bình luận (1)
){kind=link}
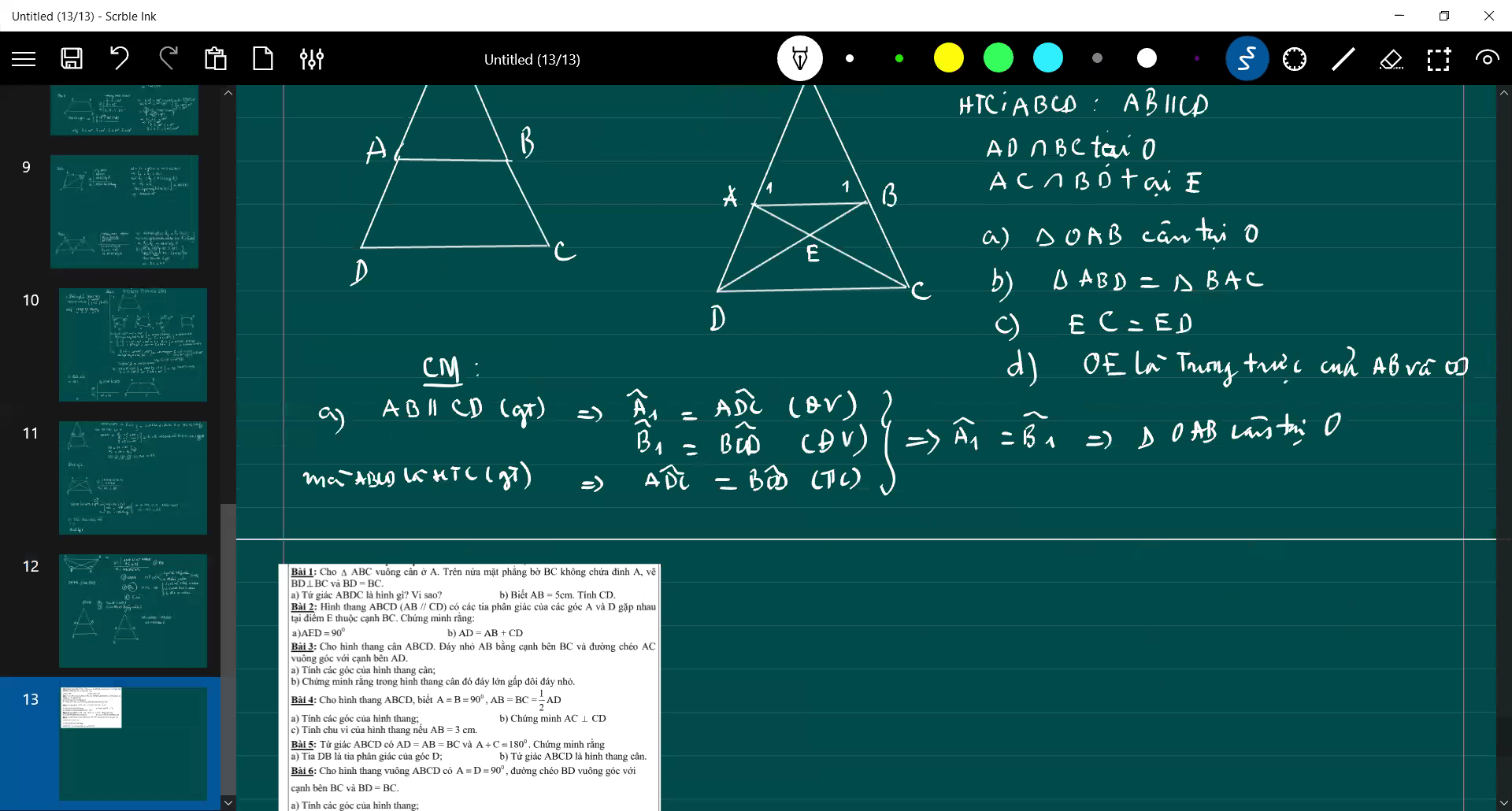
xin lỗi vì đã lm phiền mn ạ, giải hộ em với, em lm hết a với b rồi nên a chị nào giúp em câu c và d với ạ, đc sử dụng dữ kiện của câu trên nhé. GT ( đề bài ) ở bên phải hình vẽ ạ. HTC là hình thag cân ạ, còn cái (n) trong GT là cắt >< Mong mn giúp e ạ
có j thắc mắc thì mn cứ hỏi ạ, em cần trc sáng mai nhé!? ><
Đúng 0
Bình luận (0)
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED
Đúng 0
Bình luận (0)